【矩阵论】Chapter 1—向量空间知识点总结复习

1 定义

• 数域定义

  数域$F$，是至少包含$0$和$1$的数集，并满足以下性质：

  1. $\forall a\in F, -a\in F$
  2. $\forall b\in F(b\neq 0), b^{-1}\in F$
  3. $\forall a, b\in F, a+b\in F$
  4. $\forall a,b\in F, a\cdot b\in F$

  矩阵论中最常用到的两个数域是$R$（实数域）和$C$（复数域）

• 代数系统定义

  代数系统通常是定义了一些运算和运算规则的集合。描述一个代数系统需要：

  1. 一组元素
  2. 运算
  3. 运算规则

• 几何向量定义

  有大小有方向的量，可以用有向线段表示，如$\vec{\alpha}$。有加法和数乘运算。

• 向量空间定义

  一个域 $F$（底域）上的向量空间（线性空间或线性向量空间）$V$ 是一组元素（称为向量）以及加法和标量乘法这两种运算，并满足以下条件：

  1. 闭包性

     • $\forall x,y\in V, x+y\in V$，且$x+y$运算结果唯一

     • $\forall a\in F,x\in V, a\cdot x\in V$，且$a\cdot x$运算结果唯一

  2. 加法公理

     • 交换律：$\forall x,y\in V, x+y=y+x$
     • 结合律：$\forall x,y,z\in V, x+(y+z)=(x+y)+z$
     • 存在零向量：$\forall x\in V,x+0=0+x=x$
     • 存在相反向量：$\forall x\in V,\exist (-x)\in V,x+(-x)=0$

  3. 标量乘法公理

     • 结合律：$\forall a,b\in F, x\in V,a\cdot (b\cdot x)=(ab)\cdot x$
     • 分配律$1$：$\forall a\in F, x,y\in V,a\cdot(x+y)=a\cdot x+a\cdot y$
     • 分配律$2$：$\forall a,b\in F, x\in V,(a+b)\cdot x=a\cdot x + b\cdot x$
     • 存在单位元素：$\forall x\in V,1\cdot x=x$

• 向量空间重点

  定义一个向量空间需要：一个集合$V$，一个数域$F$，两种运算，八种运算规则。

• 常见向量空间

  1. $R^{m\times n},(R^{m\times 1}=R^m)$：$m\times n$的实数矩阵集合，在$R$上的向量空间
  2. $C^{m\times n},(C^{m\times 1}=R^m)$：$m\times n$的复数矩阵集合，在$C$上的向量空间
  3. $C_{[a,b]}$：闭区间上的连续函数集合，在$R$上的向量空间
  4. $P_n$：次数小于 $n$ 的实多项式的集合，在$R$上的向量空间

2 子空间

• 子空间定义

  如果$S$是向量空间$V$在数域$F$上的一个非空子集，且满足闭包性，则$S$就是$V$的一个子空间。

  由$V$的零向量所组成的自己${0}$是$V$的一个子空间，称为零子空间，向量空间$V$本身也是$V$的一个子空间，它们都称为$V$的平凡子空间，$V$的其他子空间称为非平凡子空间。

• 子空间重点

  $V$ 的子空间 $S$ 以及 $V$ 的加法和标量乘法运算满足向量空间定义中的所有条件。因此，向量空间的每个子空间本身就是一个向量空间。$S$ 的底层域与 $V$ 的底层域相同。

• 零空间定义

  设$A\in F^{m\times n},N(A)={x\in F^n|Ax=0}$，则$N(A)$为$F^n$的子空间，$N(A)$称为$A$的零空间。

• 向量的线性相关性

  设$V$是数域$F$上的线性空间，$a_1,\cdots,a_n\in F,v_1,\cdots,v_n\in V$，则$a_1v_1+\cdots+a_nv_n$就是$v_1,\cdots,v_n$的线性组合。

  若存在$n$个不全为零的数$a_1,\cdots,a_n\in F$，使得$a_1v_1+\cdots+a_nv_n=0$，则称$v_1,\cdots,v_n$线性相关，否则就称为线性无关。

  线性相关的充要条件是其中有一个向量是其余向量的线性组合

• 生成集定义

  $span(K)={v|v\texttt{是向量}K\texttt{的一个线性组合}}$，即为向量$K$的线性组合生成的集合。如果$K$是向量空间$V$中的有限集，那么$span(K)$也就是$V$的子空间。

  如果$v_1,\cdots,v_n$是向量空间$V$的向量，且$V=span{v_1,\cdots,v_n}$，则集合${v_1,\cdots,v_n}$称为$V$的生成集。

• 子空间的交集、和

  1. 设$U_1,U_2$为向量空间$V$的子空间，则$U_1\cap U_2={v|v\in U_1, v\in U_2}$，$U_1\cap U_2$也是$V$的子空间。

  2. 设$U_1,U_2$为向量空间$V$的子空间，则$U_1+U_2={v_1+v_2|v_1\in U_1,v_2\in U_2}$，$U_1+ U_2$也是$V$的子空间。

     如果$U_1=span(u_1,\cdots_,u_k),U_2=span(w_1,\cdots,w_s)$，则$U_1+U_2=span(u_1,\cdots,u_k,w_1,\cdots,w_s)$。

• 子空间的直和

  设$V_1,V_2$是向量空间$V$的两个子空间，如果和$V_1+V_2$中每一个向量$\alpha$可唯一表示成$\alpha=\alpha_1+\alpha_2,\alpha_1\in V_1,\alpha_2\in V_2$，则称和$V_1+V_2$为直和，记为$V_1+V_2$。

  和$V_1+V_2$是直和$\Longleftrightarrow$和$V_1+V_2$中零向量的表示法唯一，即若$\alpha_1+\alpha_2=0(\alpha_1\in V_1,\alpha_2\in V_2)$，则$\alpha_1=0,\alpha_2=0\Longleftrightarrow V_1\cap V_2={0}\Longleftrightarrow\dim(V_1+V_2)=\dim(V_1)+\dim(V_2)$

• 补空间定义

  如果$V=V_1\oplus V_2 $，我们则称$V_1$和$V_2$互为补空间，即$V_1$是$V_2$的补。

• 补空间定理

  如果$U$是$V$的子空间，则存在$V$的子空间$W$，使得$V=U\oplus W$

3 基、坐标和维数

• 基、坐标定义

  $n$个向量$v_1,\cdots,v_n$是向量空间$V$的一组基，当且仅当：

  1. $v_1,\cdots,v_n$线性无关
  2. $V=span(v_1,\cdots,v_n)$

  基不是唯一的，但$V$的所有基中的向量个数是相同的

  设$a$是$V$中的任一向量，则$a$可以唯一的表示为基$v_1,\cdots,v_n$的线性组合$a=k_1v_1+\cdots+k_nv_n$，其中系数$k_1,\cdots,k_n$称为$a$在基$v_1,\cdots,v_n$下的坐标，记为$(k_1,\cdots,k_n)^T$。

• 维数定义

  如果向量空间$V$的基由$n$个向量组成，则我们称$V$的维数是$n$。

• 定理

  在$n$维线性空间$V$中，任意一个线性无关的向量组$a_1,\cdots,a_r$都可以扩充为$V$的一组基。

• 维数公式

  设$U_1,U_2$为向量空间$V$的两个子空间，则

  $\dim(U_1+U_2)=\dim(U_1)+\dim(U_2)-\dim(U_1\cap U_2)$

4 基变换

• 过渡矩阵

  设$u_1,\cdots,u_n$与$v_1,\cdots,v_n$是$n$维线性空间$V$的两组基，则有如下关系 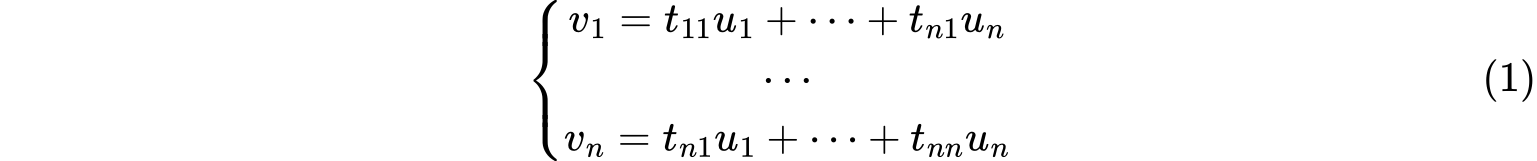关系式用矩阵表示为 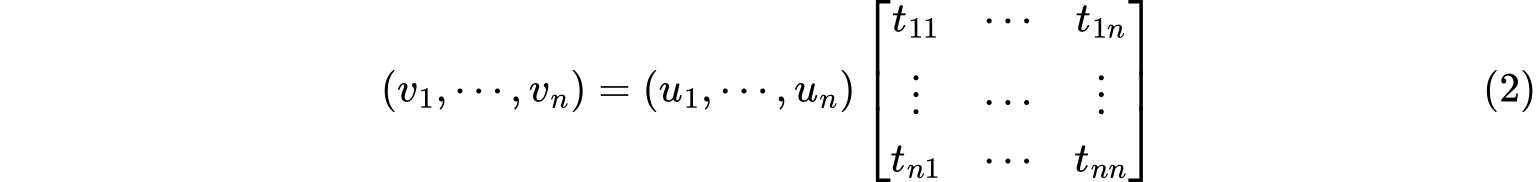$n$阶矩阵 称为由基$u_1,\cdots,u_n$到基$v_1,\cdots,v_n$的过渡矩阵。

5 行空间和列空间

• 矩阵的秩

  如果矩阵$A$的秩为$r$，则说明：

  1. 存在一个$r×r$子矩阵，其行列式不为零；和
  2. 所有的 $(r+1)\times (r+1)$ 的子矩阵的行列式为零。

• 行空间和列空间

  设$A\in F^{m\times n}$

  1. 行空间：由$A$的行向量生成的$F^{1\times n}$的子空间。（也为$A^T$的列空间）
  2. 列空间：由$A$的列向量生成的$F^{m\times 1}$的子空间。（也为$A^T$的行空间）

• 行等价条件

  矩阵$A$和$B$被称为是行等价$\Longleftrightarrow$$B$可以由$A$进行初等行变换得到。

  特别地，对于非奇异矩阵，有充要条件是存在一个非奇异矩阵$M$使得，$MA=B$。

• 行等价性质

  设矩阵$A,B$是两个行等价的矩阵，则：

  1. 它们有相同的行空间。
  2. 如果$A$中的列向量$a_{i_1},\cdots,a_{i_k}$是线性无关的，则$B$中的列向量$b_{i_1},\cdots,b_{i_k}$也是线性无关的

• 列空间性质

  1. 线性系统$Ax=b$相容（有解）$\Longleftrightarrow$$b$在$A$的列空间里
  2. $Ax=b$相容当且仅当$rank(A)=rank(A,b)$，即等价于$A$的列空间等于$(A,b)$的列空间
  3. 如果$\forall b\in F^m$，$Ax=b$相容，说明$A$的列空间是$F^m$。
  4. 如果$\forall b,Ax=b$至多只有一个解，说明$A$的列向量是线性无关的，则$A$的列向量是$A$的列空间的基，等价于$A$是非奇异矩阵。

• 秩——零度定理

  设$A$为$m\times n$矩阵，则$rank(A)+rank(N(A))=0$

• 秩和维数

  设$A$是$m\times n$矩阵，$A$的行空间维数等于$A$的列空间维数，即$\dim(R(A^T))=\dim(R(A))$，其中$R(A^T)$表示$A^T$的列空间，即$A$的行空间。

  虽然矩阵$A$的行空间和列空间不相同，但是它们有相同的维数，都为$A$的秩，矩阵$A$在初等变换下秩是不变的。