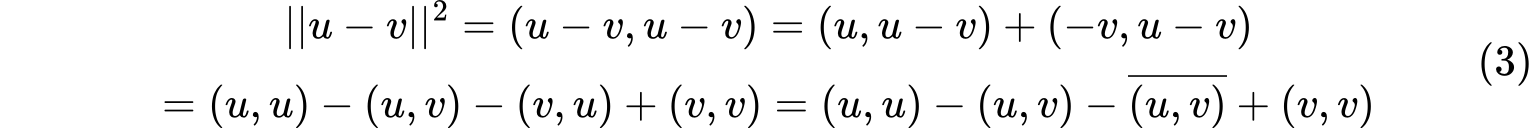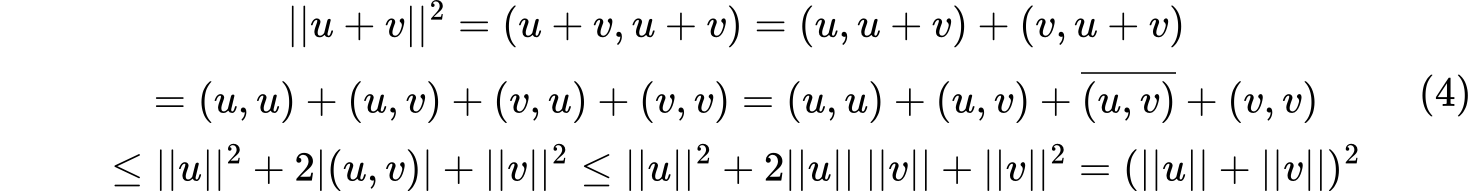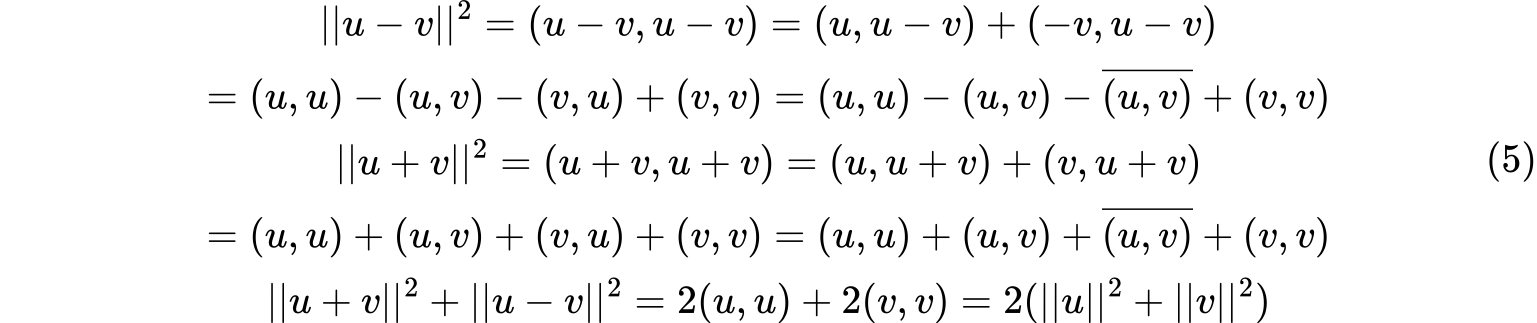【矩阵论】Chapter 2—内积空间知识点总结复习

1 内积空间

• 内积空间定义

  设$V$是在数域$F$上的向量空间，则$V$到$F$的一个代数运算记为$(\alpha,\beta)$。如果$(\alpha,\beta)$满足以下条件：

  1. $(\alpha,\beta)=\overline{(\beta,\alpha)}$（$\overline{}$表示共轭符，针对复数域，为了保证复数运算的正确性）
  2. $(\alpha+\beta,\gamma)=(\alpha,\gamma)+(\beta,\gamma)$
  3. $(k\alpha,\beta)=k(\alpha,\beta)$
  4. $(\alpha,\alpha)\geq 0$，当且仅当$\alpha=0$时，$(\alpha,\alpha)=0$。

  其中$k\in F,\alpha,\beta,\gamma\in V$。则称$(\alpha,\beta)$为$\alpha$和$\beta$的内积。定义了内积的向量空间$V$称为内积空间。特别地，称实数域$R$上的内积空间$V$为Euclid空间（欧式空间）；称复数域$C$上的内积空间$V$为酉空间。

• 标准内积

  1. 在实数域$R$上的$n$维向量空间$R^n$中，对向量$x=(x_1,\cdots,x_n)^T,y=(y_1,\cdots,y_n)^T$，定义内积

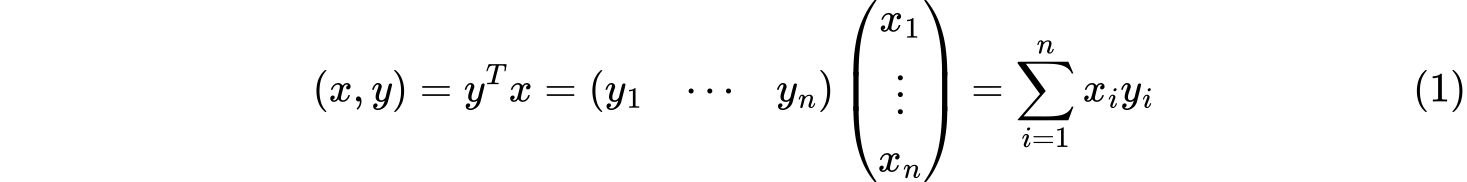
  2. 在复数域$C$上的$n$维向量空间$C^n$，对向量$x=(x_1,\cdots,x_n)^T,y=(y_1,\cdots,y_n)^T$，定义内积 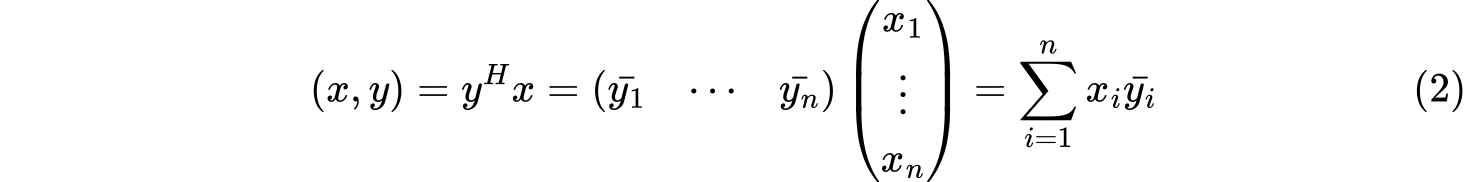其中$y^H$表示$y$的共轭转置。

  以上两个内积我们称为$R^n$或$C^n$的标准内积，一般我们探讨的也就是标准内积。

• 重要定义

  设$u,v$是内积空间$V$的向量

  1. 则$v$的长度或范数为：$||v||=\sqrt{(v,v)}$，长度为$1$的称为单位向量。如果$v\neq 0$，则$\frac{v}{||v||}$是一个单位向量
  2. 如果$v\neq 0$，则$u$在$v$上的数量投影被定义为：$\alpha=\frac{(u,v)}{||v||}$，$u$在$v$上的向量投影被定义为：$p=\alpha\frac{v}{||v||}=\frac{(u,v)}{(v,v)}v$
  3. 如果$(u,v)=0$，则称$u$和$v$正交

• 内积的基本性质

  设$u,v\in V$，其中$V$是内积空间，则

  1. 勾股定理：如果$u\perp v$，则$||u-v||^2=||u||^2+||v||^2$ 证明：

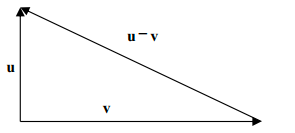
  2. 柯西不等式：$|(u,v)|\leq ||u||\space ||v||$。等式成立当且仅当$u$和$v$线性相关。 证明： 如果$u,v$线性相关，则设$u=kv,k\in F$，则$(u,v)=(kv,v)=k||v||^2$ 如果$u,v$线性无关，设$z=u-\frac{(u,v)}{(v,v)}v$，则$(z,v)=(u-\frac{(u,v)}{(v,v)}v,v)=(u,v)-\frac{(u,v)}{(v,v)}(v,v)=0$，则$z$和$v$正交。转换得到$u=z+\frac{(u,v)}{(v,v)}v$，根据正交性，结合勾股定理则$||u||^2=||z||^2+|\frac{(u,v)}{(v,v)}|^2||v||^2=||z||^2+\frac{|(u,v)|^2}{(||v||^2)^2}||v||^2=||z||^2+\frac{|(u,v)|^2}{||v||^2}$ 又因为$||z||^2> 0$（线性无关，$||z||^2$必大于$0$），则$|(u,v|<||u||\space ||v||$

  3. 三角不等式：$||u+v||^2\leq ||u||^2+||v||^2$ 证明：

  4. 平行四边形准则：$||u+v||^2+||u-v||^2=2(||u||^2+||v||^2)$ 证明：

2 标准正交向量集

• 正交向量集定义

  设$v_1,\cdots,v_n$是内积空间$V$中的非零向量，如果$V$中的任意两个向量$(v_i,v_j)=0(i\neq j)$，则$V$是一个正交向量集。

• 标准正交向量集定义

  如果$V$是一个正交向量集，且$V$中的所有向量都是单位向量，即$(v_i,v_i)=1$，则$V$是一个标准正交向量集。

• 正交向量集性质

  如果$v_1,\cdots,v_n$是内积空间$V$的一个正交向量集，则$v_1,\cdots,v_n$都是线性无关的。

• 正交基和标准正交基

  在$n$维内积空间中，由$n$个正交向量组成的基称为正交基，由$n$个标准正交向量组成的基称为标准正交基。

• 标准正交基表示向量坐标

  设$u_1,\cdots,u_n$是内积空间$V$的一个标准正交基，如果$v=\sum_{i=1}^nc_iu_i$，则$c_i=(v,u_i)$其中$c_i$为向量$v$在向量$u_i$的标量投影。

• Parseval公式

  设$u_1,\cdots,u_n$是内积空间$V$的一个标准正交基，如果$u=\sum_{i=1}^na_iu_i,v=\sum_{i=1}^nb_iu_i$，则$(u,v)=\sum_{i=1}^na_i\bar{b_i}$。并且，$||v||^2=\sum_{i=1}^n b_i\bar{b_i}=\sum_{i=1}^n|b_i|^2$。

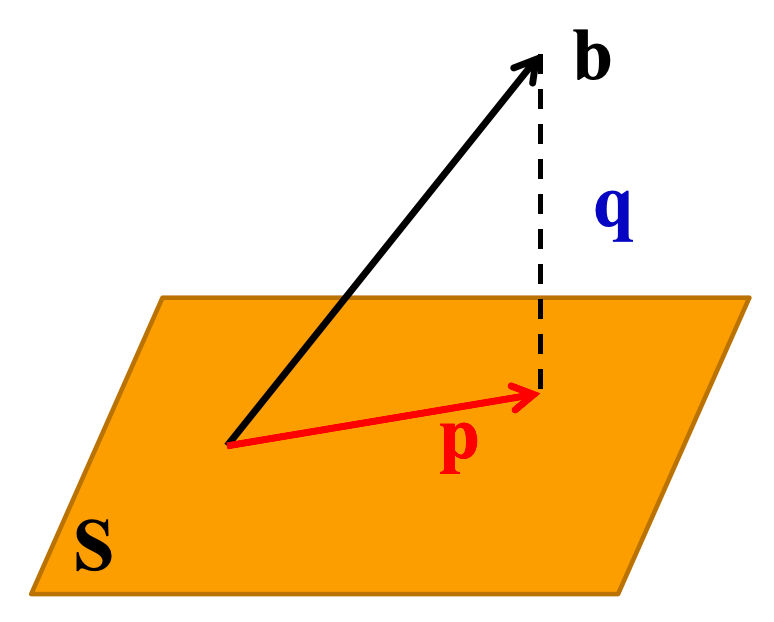
• 正交投影向量定义

  如果$S$是内积空间$V$的子空间，令$b\in V$，如果存在向量$p\in S,q$，使得$q\perp S,b=p+q$，则称$p$是$b$在子空间$S$上的正交投影向量。

  

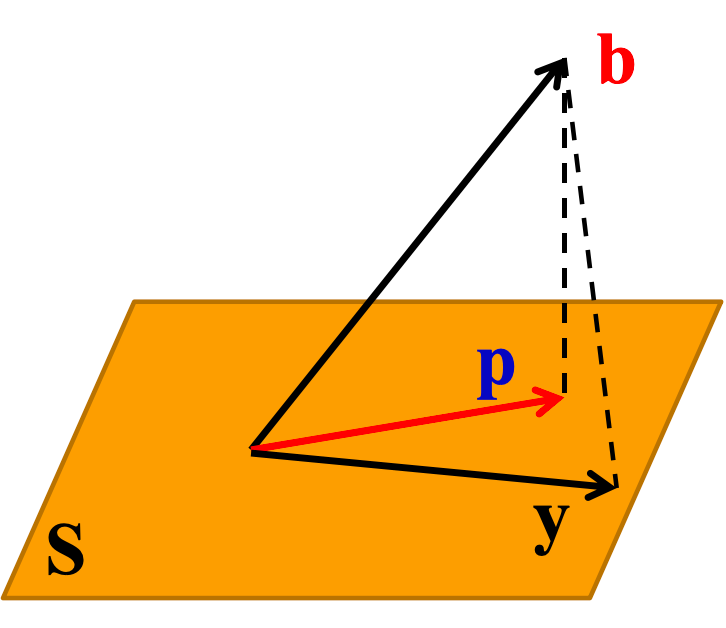
  设$u_1,\cdots ,u_n$为$S$的标准正交基，如果$p=\sum_{i=1}^n(b,u_i)u_i$，则

  1. $b-p$与$s$的任意一个向量正交

  2. $p$是$S$中唯一一个最接近$b$的向量。也就是说$\forall y\in S,y \neq p$，有$||y-b||>||p-b||$。向量$p$是$b$在子空间$S$上的正交投影向量。

     

• 投影矩阵

  设$S$是内积空间$F^n$的非零子空间，$b\in F^n$，$u_1,\cdots,u_n$为$S$的标准正交基，$U={u_1,\cdots,u_n}$，则$b$在子空间$S$的正交投影$p=UU^Hb$，其中$U$则是投影矩阵。

3 Gram-Schmidt正交化方法

设$\alpha_1,\cdots,\alpha_n$是向量空间$V$的线性无关向量组。我们按照以下步骤标准正交化得到标准正交向量组$\beta_1,\cdots,\beta_n$

1. 单位化向量$\alpha_1$，得到$\beta_1=\frac{\alpha_1}{||\alpha_1||}$。易知$span(\alpha_1)=span(\beta_1)$。
2. 找到$\alpha_2$在$span(\beta_1)$上的向量投影$p_1=(\alpha_2,\beta_1)\beta_1$，根据推导可知$\alpha_2-p_1$和$span(\beta_1)$正交。我们对其单位化得到$\beta_2=\frac{\alpha_2-p_1}{||\alpha_2-p_1||}$。易得$span(\alpha_1,\alpha_2)=span(\beta_1,\beta_2)$。
3. 找到$\alpha_3$在$span(\beta_1,\beta_2)$上的向量投影$p_2=(\alpha_3,\beta_1)\beta_1+(\alpha_3,\beta_2)\beta_2$，根据推导可知$\alpha_3-p_2$和$span(\beta_1,\beta_2)$正交。我们对其单位化得到$\beta_3=\frac{\alpha_3-p_2}{||\alpha_3-p_2||}$。易得$span(\alpha_1,\alpha_2,\alpha_3)=span(\beta_1,\beta_2,\beta_3)$。
4. 如上进行操作，$\alpha_i$在$S_{i-1}=span(\alpha_1,\cdots,\alpha_i)=span(\beta_1,\cdots,\beta_i)$的向量投影$p_{i-1}=(\alpha_i,\beta_1)\beta_1+\cdots+(\alpha_i,\beta_{i-1})\beta_{i-1}$，则$\alpha_i-p_{i-1}$和$S_{i-1}$正交。所以对其单位化得到$\beta_i=\frac{\alpha_i-p_{i-1}}{||\alpha_i-p_{i-1}||}$。易得$span(\alpha_1,\cdots,\alpha_{i})=span(\beta_1,\cdots,\beta_{i})$。
5. 直到求得$\beta_n$，得到标准正交向量组$\beta_1,\cdots,\beta_n$

4 正交子空间

• 正交子空间定义

  $X,Y$是内积空间$V$的子空间，如果$\forall x\in X,y\in Y$，$(x,y)=0$，则$X$和$Y$正交，我们记作$X\perp Y$。

• 正交补定义

  设$Y$是内积空间$V$的子空间，则$V$中与$Y$的每个向量正交的所有向量称为$Y^{\perp}$，$Y^\perp ={x\in V|\forall y\in Y,(x,y)=0 }$。

• 正交子空间定理

  如果$V_1$和$V_2$正交，则$V_1+V_2$的和为直和。

• 正交补性质

  设$S$为有限维内积空间$V$的子空间，则：

  1. $V=S\oplus S^\perp$。并且如果$V=S\oplus W,W\perp S$，则$W=S^\perp$。
  2. $(S^{\perp})^{\perp}=S$

• 向量到子空间的最小距离

  设$S$为有限维内积空间$V$的子空间，$\forall b\in V$，则$S$ 中的给定向量 $p$ 与给定向量$b$ 最接近，当且仅当$b-p\perp S^{\perp}$。即$p$是$b$在$S$上的向量投影。

• 矩阵的基本子空间

  设$A$为$m\times n$矩阵，则

  $N(A)={x\in F^n|Ax=0}$：$A$的零空间，$F^n$的子空间。

  $R(A)={Ax|x\in F^n}$：$A$的列空间，$F^m$的子空间。

  $N(A^H)$：$A^H$的零空间，$F^m$的子空间。

  $R(A^H)$：$A^H$的列空间，$F^n$的子空间。

  $N(A)=R(A^H)^\perp,N(A^h)=R(A)^\perp$

  $F^n=N(A)\oplus N(A)^\perp=N(A)\oplus R(A^H)$

  $\dim(F^n)=\dim(N(A))+\dim(R(A^H))$

5 最小二乘问题

• 问题定义

  设线性系统$Ax=b$，其中$A\in F^{m\times n}$，可能不相容（无解）。我们能否找到一个最佳解，即向量$\hat{x}$使得$A\hat{x}-b=\min_{x\in F^n}||Ax-b||$

• 问题核心

  找到向量$\hat{x}$即是使得$A\hat{x}$等于$b$在$R(A)$上的向量投影。

  

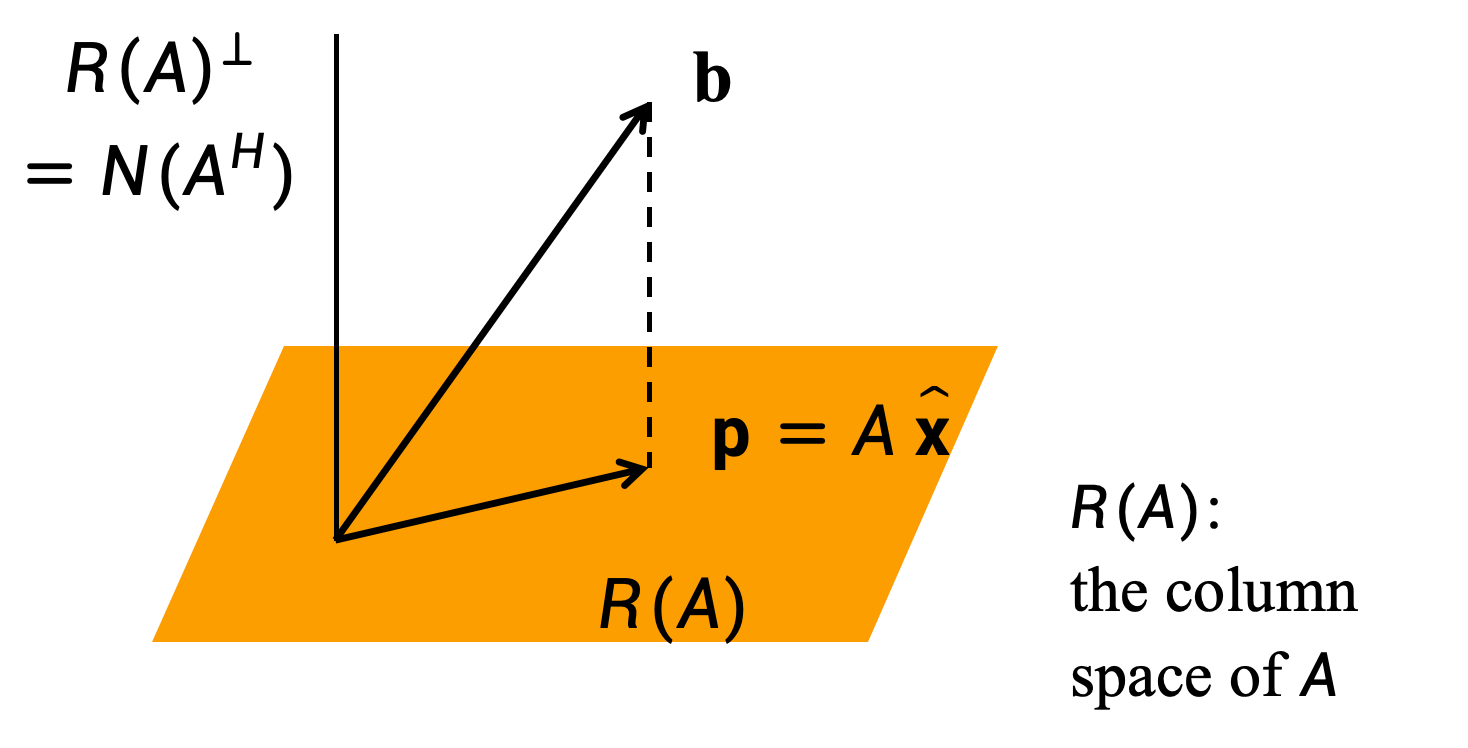
• 最小二乘解等价条件

  1. $\hat{x}$是$Ax=b$的最小二乘解
  2. $A\hat{x}-b=\min_{x\in F^n}||Ax-b||$
  3. $A\hat{x}$等于$b$在$R(A)$上的正交向量投影
  4. $A\hat{x}-b\in R(A)^\perp =N(A^H)$
  5. $A^H(A\hat{x}-b)=0$
  6. $A^HA\hat{x}=A^Hb$（正规方程）

• 正规方程的相容性

  设$A\in F^{m\times n}$，则正规方程$A^HAx=A^Hb$有解，其为$Ax=b$的最小二乘解。

  最小二乘解不唯一，但是对于任意解$x,y$，$Ax=Ay$，且$Ax$和$Ay$都是$b$在$R(A)$上的向量投影。

• 最小二乘解唯一解

  设$A\in F^{m\times n}$，且$rank(A)=n$（列满秩），$b\in F^n$，则正规方程$A^HAx=A^Hb$有唯一解$\hat{x}=(A^HA)^{-1}A^Hb$。$\hat{x}$为$Ax-b$的唯一最小二乘解。

6 正交矩阵和酉矩阵

• 正交矩阵定义

  设$A\in R^{n\times n}$，$A$的所有列向量构成$R^n$的标准正交集，具有$R^n$上的标准内积。

• 酉矩阵定义

  设$A\in C^{n\times n}$，$A$的所有列向量构成$C^n$的标准正交集，具有$C^n$上的标准内积。

  易知，正交矩阵也是酉矩阵。

• 正交矩阵和酉矩阵的充要条件

  $A$是正交矩阵当且仅当$A^TA=I$

  $A$是酉矩阵当且仅当$A^HA=I$

• 若$A\in C^{n\times n}$，则以下条件等价

  1. $A$是酉矩阵
  2. $A$的列向量构成$C^n$的标准正交集
  3. $A^HA=I$
  4. $A^{-1}=A^H$
  5. $\forall x,y \in C^n,(Ax,Ay)=(x,y)$
  6. $\forall x\in C^n,(Ax,Ax)=(x,x)$