数据结构与算法 面试题目总结
1 排序算法
| 排序算法 | 平均时间复杂度 | 最差时间复杂度 | 空间复杂度 | 数据对象稳定性 | 算法基本思路 |
|---|---|---|---|---|---|
| 冒泡排序 | $$O(n^2)$$ | $$O(n^2)$$ | $$O(1)$$ | 稳定 | 反复交换相邻逆序的元素,直到没有逆序对 |
| 选择排序 | $$O(n^2)$$ | $$O(n^2)$$ | $$O(1)$$ | 数组不稳定、链表稳定 | 反复选择未排序部分中的最小(大)元素,放在已排序部分的末尾 |
| 插入排序 | $$O(n^2)$$ | $$O(n^2)$$ | $$O(1)$$ | 稳定 | 逐一选择未排序元素,将其插入到已排序部分的正确位置 |
| 快速排序 | $$O(n \log_2 n)$$ | $$O(n^2)$$ | $$O(\log_2 n)$$ | 不稳定 | 选择基准,将数组分为小于和大于基准的两部分,递归排序 |
| 堆排序 | $$O(n \log_2 n)$$ | $$O(n \log_2 n)$$ | $$O(1)$$ | 不稳定 | 构建最大(小)堆,将堆顶元素与末尾元素交换,调整堆 |
| 归并排序 | $$O(n \log_2 n)$$ | $$O(n \log_2 n)$$ | $$O(n)$$ | 稳定 | 递归地将数组分为两部分,分别排序后合并 |
| 希尔排序 | $$O(n \log_2 n)$$ | $$O(n^2)$$ | $$O(1)$$ | 不稳定 | 分组进行插入排序,逐渐减少间隔,直到间隔为1 |
| 计数排序 | $$O(n + m)$$ | $$O(n + m)$$ | $$O(n + m)$$ | 稳定 | 统计每个元素的出现次数,根据计数对元素进行排序 |
| 桶排序 | $$O(n)$$ | $$O(n)$$ | $$O(m)$$ | 稳定 | 将元素分配到不同的桶中,分别排序后合并 |
| 基数排序 | $$O(k \cdot n)$$ | $$O(n^2)$$ | 取决于实现 | 稳定 | 逐位排序,从最低有效位到最高有效位进行 |
2 栈与队列的区别
- 队列(Queue):是限定只能在表的一端进行插入和在另一端进行删除操作的线性表;
- 栈(Stack):是限定只能在表的一端进行插入和删除操作的线性表。
- 队列先进先出,栈先进后出。
- 栈只能在表尾插入删除,队列在表尾插入表头删除。
- 应用场景不同:
- 栈:括号问题的求解等
- 队列:计算机系统中各种资源的管理等。
- 遍历速度不同:
- 队列:基于地址指针进行遍历,而且可以从头部或者尾部进行遍历,但不能同时遍历,无需开辟空间,因为在遍历的过程中不影响数据结构,所以遍历速度要快;
- 栈:只能从顶部取数据,也就是说最先进入栈底的,需要遍历整个栈才能取出来,而且在遍历数据的同时需要为数据开辟临时空间,保持数据在遍历前的一致性。
3 两个栈实现一个队列
使用两个栈来实现一个队列,可以有效地利用栈的特性(后进先出)来模拟队列的特性(先进先出)。我们可以使用两个栈来分离入队和出队操作,具体实现步骤如下:
- 栈1(
stack1)用于处理入队操作。 - 栈2(
stack2)用于处理出队操作。
- 入队列:直接压入元素至
stack1即可 - 出队列:如果
stack2不为空,把stack2中的栈顶元素直接弹出。否则,把stack1的所有元素全部弹出压入stack2中,再弹出stack2的栈顶元素
| |
4 两个队列实现栈
使用两个队列来实现一个栈,可以利用队列的特性(先进先出)来模拟栈的特性(后进先出)。我们可以使用两个队列来分离入栈和出栈操作,具体实现步骤如下:
- 队列1(
queue1)用于存储元素。 - 队列2(
queue2)作为辅助队列用于操作元素。
- 入栈操作:将元素直接入队到
queue1中。 - 出栈操作:
- 将
queue1中的所有元素(除了最后一个)逐个出队并入队到queue2中。 - 最后一个元素是栈顶元素,将其出队。
- 交换
queue1和queue2,以保持queue1始终为主队列。
- 将
| |
5 链表与数组的区别
- 数组静态分配内存,链表动态分配内存;。
- 数组在内存中连续,链表不连续。
- 数组利用下标定位,时间复杂度为O(1),链表定位元素时间复杂度O(n)。
- 数组插入或删除元素的时间复杂度O(n),链表的时间复杂度O(1)。
- 数组元素在栈区,链表元素在堆区。
6 什么是堆?
如果一棵完全二叉树的任意一个非终端结点的元素都不小于其左儿子结点和右儿子结点(如果有的话) 的元素,则称此完全二叉树为最大堆。
同样,如果一棵完全二叉树的任意一个非终端结点的元素都不大于其左儿子结点和右儿子结点(如果 有的话)的元素,则称此完全二叉树为最小堆。
最大堆的根结点中的元素在整个堆中是最大的;
最小堆的根结点中的元素在整个堆中是最小的。
7 什么是二叉排序树
二叉排序树(Binary Sort Tree)又称二叉查找树(Binary Search Tree),亦称二叉搜索树。
二叉排序树或者是一棵空树,或者是具有下列性质的二叉树:
- 若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
- 左、右子树也分别为二叉排序树;
- 没有键值相等的节点
二分查找的时间复杂度是O(log(n)),最坏情况下的时间复杂度是O(n)(相当于顺序查找)
8 什么是平衡二叉树?
平衡二叉树(balanced binary tree),又称 AVL 树。它或者是一棵空树,或者是具有如下性质的二叉树:
- 它的左子树和右子树都是平衡二叉树,
- 左子树和右子树的深度之差的绝对值不超过1。
平衡二叉树是对二叉搜索树(又称为二叉排序树)的一种改进。二叉搜索树有一个缺点就是,树的结构是无法预料的,随意性很大,它只与节点的值和插入的顺序有关系,往往得到的是一个不平衡的二叉树。在最坏的情况下,可能得到的是一个单支二叉树,其高度和节点数相同,相当于一个单链表,对其正常的时间复杂度有O(log(n))变成了O(n),从而丧失了二叉排序树的一些应该有的优点。
旋转是平衡二叉树维护平衡性的核心操作,包括以下几种:
- 单右旋转(Right Rotation):用于修复左子树过高的情况。
- 单左旋转(Left Rotation):用于修复右子树过高的情况。
- 双旋转(Double Rotation):包括先左后右旋转和先右后左旋转,用于修复特定的不平衡情况。
9 什么是B树
B树是一种自平衡的多路查找树,其中每个节点可以有多个子节点和多个键。B树具有以下特性:
- 节点包含多个键和子节点:每个节点可以存储多个键和子节点。节点中的键按照递增顺序存储。
- 根节点至少有两个子节点(如果不是叶节点)。
- 内部节点的子节点数受限:一个内部节点至少有$$[m/2]$$个子节点,最多有 $$m$$个子节点(这里的$m$是B树的阶)。
- 所有叶子节点处于同一层:B树的所有叶子节点都在同一层,保证树的平衡性。
B树的性质如下:
- 平衡性:B树是自平衡的,所有叶子节点处在同一层,树的高度通常较小,因而能够保证较快的搜索、插入和删除操作。
- 高效的磁盘I/O操作:由于节点可以包含多个键和子节点,B树通常用于磁盘存储中,减少磁盘I/O操作的次数。
- 时间复杂度:搜索、插入和删除操作的时间复杂度均为$O(\log n)$,其中$n$是树中的键的总数。
B树的操作如下:
- 搜索:从根节点开始,根据当前节点中的键范围,递归或迭代地选择相应的子节点进行搜索,直到找到目标键或到达叶子节点。
- 插入:
- 在叶子节点插入新键。
- 如果叶子节点已满,则进行分裂操作,将中间键提升到父节点,并将叶子节点分裂为两个节点。
- 如果父节点也满,则递归进行分裂,直到树根。
- 删除:
- 从树中删除键。
- 如果删除键导致节点下溢(键数少于$[m/2]$),则进行合并或借用操作,以保持B树的平衡性。
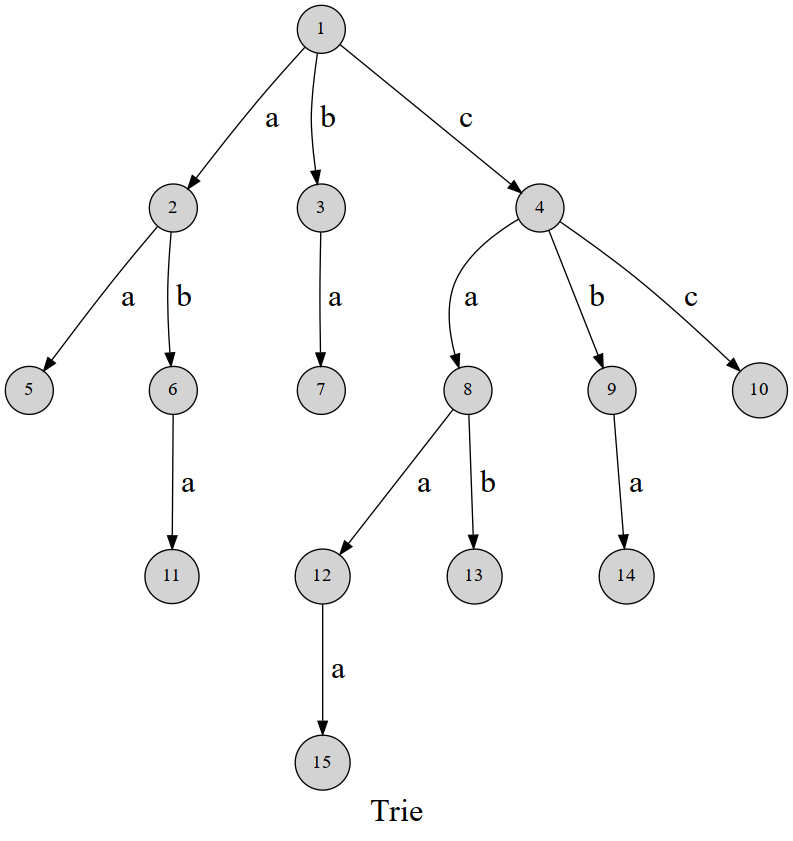
10 Trie 树
Trie 树,又称前缀树,字典树, 是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
Trie 树查询和插入时间复杂度都是 O(n),是一种以空间换时间的方法。当节点树较多的时候,Trie 树占用的内存会很大。
Trie 树常用于搜索提示。如当输入一个网址,可以自动搜索出可能的选择。当没有完全匹配的搜索结果,可以返回前缀最相似的可能。
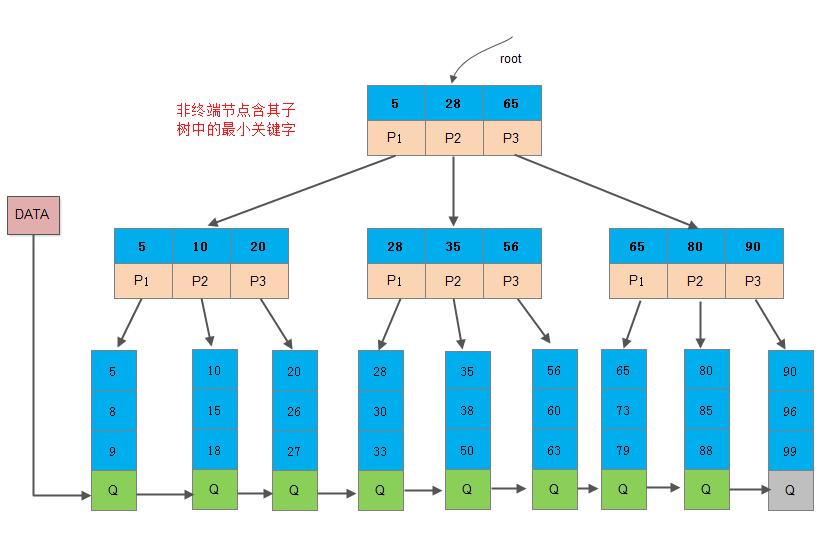
11 B+树
B+树通常用于数据库和操作系统的文件系统中,B+树的结构如下:
- 根节点(Root Node):B+树的根节点可以是叶子节点,也可以是内部节点。
- 内部节点(Internal Nodes):存储键值用于导航,不存储实际数据。每个内部节点包含若干个键和指向子节点的指针。
- 叶子节点(Leaf Nodes):存储所有的实际数据,并且包含指向相邻叶子节点的指针,形成一个双向链表。
B+树的性质:
- 有序性:所有键按升序排列。
- 平衡性:树的所有叶子节点处于同一层级,保证了平衡性。
- 多路性:每个节点可以有多个子节点,具体数量由树的阶(order)决定。
B+树的操作:
- 查找(Search):从根节点开始,依次比较键值,沿着指向子节点的指针递归查找,直到找到目标叶子节点。
- 插入(Insert):将新键插入适当的叶子节点,如果叶子节点满了,则分裂叶子节点并将中间键上移到父节点,递归进行分裂直到树恢复平衡。
- 删除(Delete):从叶子节点删除键,如果删除导致节点键数目不足,则进行节点合并或键重新分配,直到树恢复平衡。
B+树的优点:
- 高效的范围查询:由于所有数据都存储在叶子节点中,并且叶子节点形成双向链表,B+树能够高效地进行范围查询(range query)。
- 高存储利用率:内部节点只存储键,数据存储在叶子节点中,节点分裂和合并更加高效。
- 低树高(Tree Height):B+树的多路性使得其树高较低,查找、插入和删除操作的时间复杂度为$O(\log_mn$,其中$m$为树的阶。
12 什么是红黑树?
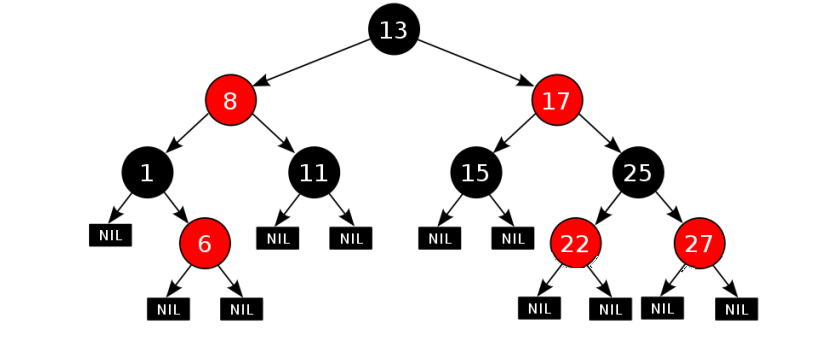
红黑树(为了解决平衡树在插入、删除等操作需要频繁调整的情况)是一种自平衡的二叉查找树(BST),广泛用于计算机科学中实现高效的数据存储和检索。它通过在每个节点上附加一个颜色属性(红或黑)来保持树的平衡,从而确保树的高度在对数级别,提供较好的时间复杂度性能。
红黑树的性质:
- 每个结点不是红色就是黑色;
- 根节点是黑色的;
- 叶子节点(NIL节点)是黑色:红黑树中的叶子节点,即树尾端的所有NULL节点,都是黑色的。
- 红色节点的父节点和子节点必须是黑色的,即不能有两个连续的红色节点。
- 从任一节点到其每个叶子的所有路径包含相同数量的黑色节点:这保证了没有一条路径会比其他路径长出太多,从而确保了树的平衡。
红黑树的操作:红黑树的操作包括插入、删除和查找,基本的操作步骤与普通的二叉查找树类似,但在维护平衡性方面有所不同。
插入操作
普通BST插入:按二叉查找树的插入规则,将新节点插入适当位置。
节点染色为红色:新插入的节点初始为红色。
调整平衡:通过旋转和重新染色来保持红黑树的性质。
情况1:插入节点的父节点是黑色:不需要进一步操作。
情况2:插入节点的父节点是红色:根据叔节点的颜色,有不同的调整方法,包括重新染色和旋转。
删除操作
普通BST删除:按二叉查找树的删除规则,找到并删除节点。
调整平衡:删除节点后可能破坏红黑树的性质,需要通过旋转和重新染色来恢复平衡。
情况1:删除节点是红色:不需要进一步操作。
情况2:删除节点是黑色:通过双重黑色节点的概念和调整,包括重新染色和旋转,来恢复红黑树的平衡。
红黑树的优点:
- 自平衡:通过颜色属性和旋转操作,红黑树可以保持平衡,确保基本操作的时间复杂度为$$O(\log n)$$。
- 高效查找:由于平衡性,红黑树在最坏情况下的高度为$$2\log(n+1)$$,保证了查找操作的高效性。
- 高效插入和删除:插入和删除操作在进行平衡调整时,旋转和重新染色的成本较低,确保了高效性。
红黑树广泛应用于许多计算机系统和软件中,包括:
- 关联容器:C++的STL中的map和set,Java的TreeMap和TreeSet都基于红黑树实现。
- 内存管理:Linux内核中的内存管理使用红黑树来管理空闲内存块。
- 数据库索引:一些数据库系统使用红黑树作为索引结构,实现高效的数据检索。
13 什么是哈希表?哈希表的实现方式?怎么避免哈希冲突
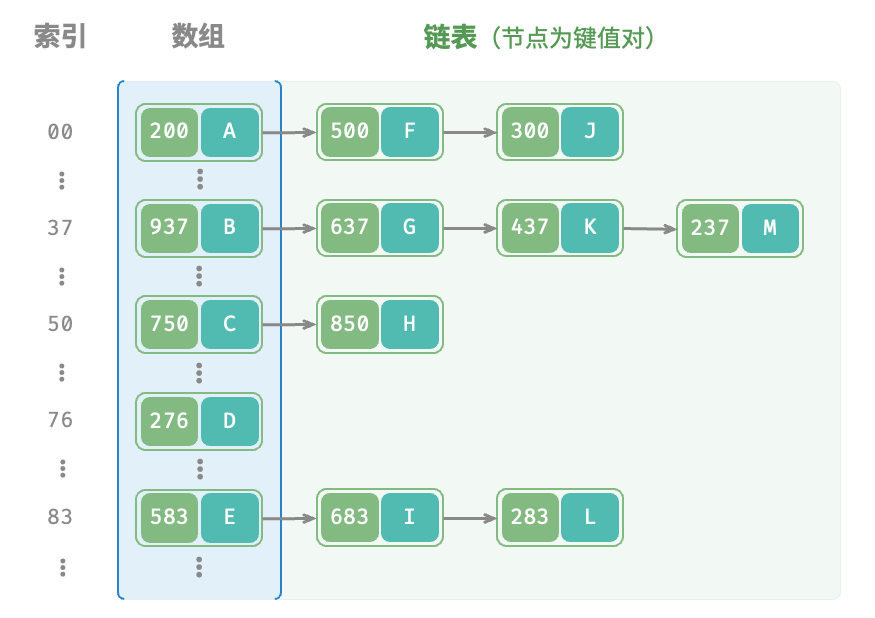
哈希表(Hash Table,也叫散列表),是根据键值 (Key-Value) 而直接进行访问的数据结构。也就是说,它通过把键值映射到表中一个位置来访问记录,以加快查找的速度。哈希表的实现主要需要解决两个问题,哈希函数和冲突解决。
哈希函数也称为散列函数,它接受一个键作为输入,并将其映射到哈希表的一个位置上。理想的哈希函数应该能够将键均匀地分布到哈希表的不同位置上,同时具有良好的计算效率。常见的哈希函数包括取余法、乘法哈希法、MD5、SHA等。选择合适的哈希函数取决于应用场景和性能要求。
当两个不同的键经过哈希函数映射后得到相同的位置时,就会发生哈希冲突。为了解决这个问题,常见的冲突解决方法包括:
- 开放定址法(Open Addressing):当发生冲突时,顺序地查找下一个可用的位置,直到找到一个空槽位。常见的开放定址法包括线性探测、二次探测、双重哈希等。
- 链地址法(Chaining)(最常用):将哈希表的每个槽位都连接一个链表(或其他数据结构),当发生冲突时,将冲突的元素插入到对应位置的链表中。这样,相同哈希值的元素都存储在同一个链表中。
- 再哈希法(Rehashing):使用另一个哈希函数计算新的哈希值,然后再次查找空槽位。这样可以减少冲突的概率,提高哈希表的性能。
- 建立公共溢出区:将哈希表的一部分空间作为溢出区,当发生冲突时,将冲突的元素存储在溢出区中。这样,哈希表的主要部分仍然保持较低的负载因子,提高了性能。
相关内容
- C/C++ 面试题目总结
- 【MIT 6.5840(6.824)学习笔记】GFS
- 【MIT 6.5840(6.824)学习笔记】 测试分布式系统的线性一致性
- 【MIT 6.5840(6.824)学习笔记】使用Go进行线程和RPC编程
- 【MIT 6.5840(6.824) 】Lab2:Key/Value Server 设计实现
 支付宝
支付宝 微信
微信