【MIT 6.5840(6.824)学习笔记】 测试分布式系统的线性一致性

Testing Distributed Systems for Linearizability 原文

1 引言

正确实现一个分布式系统是非常有挑战的一件事情，因为需要很好的处理并发和失败这些问题。网络包可能被延迟，重复，乱序或者丢弃，机器可能在任何时候宕机。即使一些计被论文证明是正确的，也仍然很难再实现中避免 bug。

除非我们使用形式方法，不然，即使我们假设实现是正确的，我们也需要去测试系统。测试分布式系统也是一件非常有挑战的事情。并发和不确定性使得我们在测试的时候非常难抓住 bug，尤其是在一些极端情况下面才会出现的 bug，譬如同时机器宕机或者极端网络延迟。

2 正确性

在讨论测试分布式系统的正确性之前，我们首先定义下什么是 “正确性”。即使对于一些简单的系统，要完全的确定系统符合预期也是一件相当复杂的事情。

考虑一个简单的 key-value store，譬如 etcd，支持两个操作：Put(key, value) 和 Get(key)，首先，我们需要考虑它在顺序情况下面的行为。

2.1 顺序规范

通常对于一个 key-value store，我们对于它在顺序操作下面的行为都能有一个直观的认识：Get 操作如果在 Put 的后面，那么一定能得到 Put 的结果。譬如，如果 Put("x", "y") ，那么后面的 Get("x") 就能得到 “y”，如果得到了 “z”，那么这就是不对的。

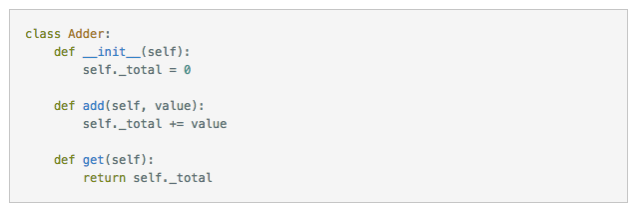
我们使用 Python 定义一个简单的 key-value store：

上面的代码比较简单，但包含了足够的信息，包括初始状态是怎样的，内部状态是如何被操作的结果改变的，从 key-value存储里面操作返回的结果是怎样的。这里需要留意下 Get() 对于不存在的 key 的处理，通常会返回一个空字符串。

3 线性一致性

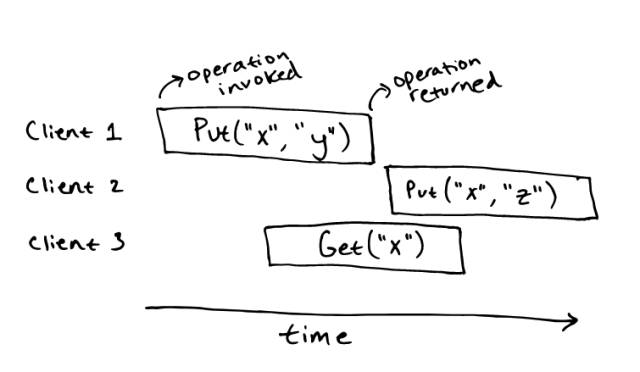
接下来，我们来考虑我们的 key-value store在并发下面会有怎样的行为。需要注意顺序规范并没有指明在并发操作下面会发生什么。譬如，顺序规范并没有说 key-value store 在下面这个场景下可以允许的操作。

我们并不能立刻知道 Get("x") 这个操作会允许返回怎样的结果。直觉上，我们可以说Get("x") 是跟 Put("x", "y") 和 Put("x", "z") 一起执行的，所以它能可能返回一个值，甚至也可能返回 ""。 如果有另一个 Get("x") 的操作在更后面执行，我们可以说这个一定能返回 "z"，因为它是最后一次写入的值，而且那个时候并没有其他的并发写入。

对于一个基于顺序规范的并发操作来说，我们会用一个一致性模型，也就是线性一致性来说明它的正确性。在一个线性一致性的系统里面，任何操作都可能在调用或者返回之间原子和瞬间执行。除了线性一致性，还有一些其他一致性的模型，但多数分布式系统都提供了线性一致性的操作：线性一致性是一个强的一致性模型，并且基于线性一致性系统，很容易去构建其他的系统。考虑到如下对 key-value store 操作的历史例子：

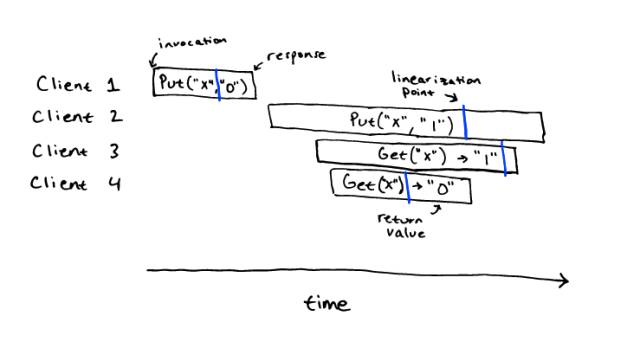
这个历史是一个线性的。在下面图片的蓝色地方，我们现实的标明了线性一致的点。这个顺序历史 Put("x", "0"), Get("x") -> "0", Put("x", "1"), Get("x") -> "1"，对于顺序规范来说就是一个正确的历史。

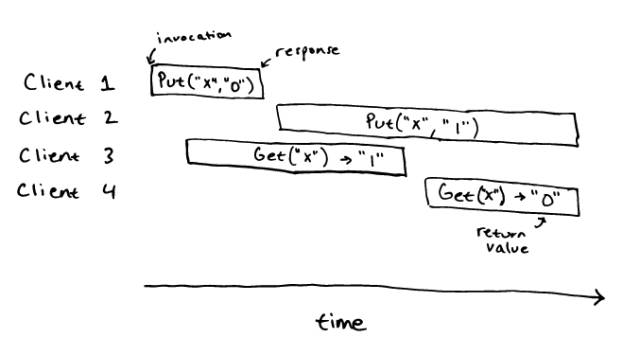
对应的，下面的历史就不是线性一致的。

对于顺序规范来说，这个历史并不是线性一致的：我们并不能在这个历史的操作里面指定出线性一致的点。我们可以画出 client 1，2 和 3 的，但我们并不能画出 client 4 的，因为这明显是一个过期的值。类似的，我们可以画出 client 1，2 和 4 的，那么 client 2 的操作一定会在 4 的操作开始的后面，但这样我们就不能处理 client 3，它只可能合法的返回 ""或者 "0"。

4 测试

有了一个正确性的定义，我们就可以考虑如何去测试分布式系统了。通常的做法就是对于正确的操作，不停的进行随机的错误注入，类似机器宕机，网络隔离等。我们甚至能模拟整个网络，这样我们就能做长时间的网络延迟等。因为测试时随机的，我们需要跑很多次从而确定一个系统的实现是正确的。

4.1 临时测试

我们实际如何做正确操作的测试呢？在最简单的软件里面，我们可以使用输入输出测试，譬如 assert(expected_output == f(input))，我们也可以在分布式系统上面使用一个类似的方法，譬如，对于 key-value store，当多个 client 开始执行操作的时候，我们可以有如下的测试：

如果测试挂掉了，那么这个系统一定不是线性一致性的，当然，这个测试并不是很完备，因为有可能不是线性一致的系统也可能通过这个测试。

4.2 线性一致性

一个更好的办法就是并发的客户端完全跑随机的操作。譬如，循环的去调用 kvstore.put(rand(), rand()) 和 kvstore.get(rand())，有可能会只用很少的 key 去增大冲突的概率。但在这种情况下，我们如何定义什么是正确的操作呢？在上面的简单的测试里面，因为每个 client 都操作的是一个独立的 key，所以我们可以非常明确的知道输出结果。

但是 clients 并发的操作同一堆 keys，事情就变得复杂了。我们并不能预知每个操作的返回值因为这并没样一个唯一的答案。但我们可以用另一个办法：我们可以记录整个操作的历史，然后去验证这个操作历史是线性一致的。

4.2.1 线性一致性验证

一个线性一致性验证器会使用一个顺序规范和一个并发操作的历史，然后执行一个判定程序去检查这个历史在规范下面是否线性一致。

4.2.2 NP 完备

但不幸的是，线性一致性验证是 NP 完备的。这个证明非常简单：我们能说明线性一致性验证是 NP 问题，并且也能展示一个 NP 困难问题能被简化成线性一致性验证。明显的，线性一致性验证是 NP 问题，譬如，所有操作的线性一致性点，根据相关的顺序规范，我们可以在多项式时间里验证。

为了说明线性一致性验证是 NP 困难的，我们可以将子集合问题简化成线性一致性验证。对于子集合问题，我们给出非负数的集合 $S={s_1,s_2,…,s_n}$ 和目标结果 $t$，然后我们必须确定是否存在一个子集 $S$ 的和等于 $t$。我们可以将这个问题简化成如下的线性一致性验证。考虑顺序规范：

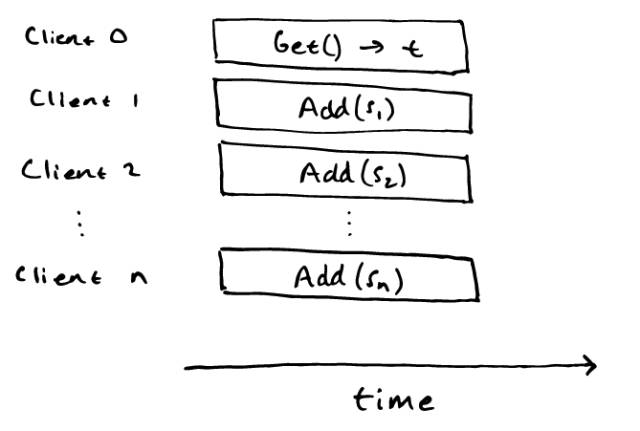
以及历史：

当且仅当子集和问题的答案为“是”时，该历史才可线性化。如果历史是可线性化的，那么我们可以采用在 Get() 操作之前具有线性化点的所有操作 Add(s_i) ，并且这些操作对应于中的元素 $s_i$总和为 $t$ 的子集。如果该集合确实有一个总和为$t$的子集，那么我们可以通过与子集中的元素$s_i$对应的操作 Add(s_i) 来构造线性化放置在 Get() 操作之前，并使其余操作发生在 Get() 操作之后。

4.2.3 实现

即使线性一致性验证是 NP 完全的，在实际中，它仍然能在一些小的历史上面很好的工作。线性一致性验证器的实现会用一个可执行的规范，加上一个历史，执行一个搜索过程去构造一个线性化，并使用一些技巧来限制减少搜索的空间。

现有的线性化检查器如 Knossos，用于 Jepsen 测试系统。但不幸的是，在测试一些分布式 key-value store 的时候，Knossos 并不能很好的工作，它可能只能适用于一些少的并发 clients，以及只有几百的事件的历史。但在一些测试里面，有很多的 clients，以及会生成更多的历史事件。

为了解决 Knossos 的问题，作者开发了 Procupine，一个用 Go 写的更快的线性一致性验证工具。Porcupine 使用一个用 Go 开发的执行规范去验证历史是否是线性的。根据实际测试的情况，Porcupine 比 Knossos 快很多倍。

Procupine Github

4.2.4 效果

使用故障注入和线性化检查来测试可线性化分布式系统是一种有效的方法。

作为对比，在使用专门的测试用 Porcupine 测试 key-value store 的时候，作者使用了这两种方式。作者在实现它自己的 key-value store 的时候引入不同的设计错误，譬如在修改之后会出现过期读，来看这些测试是否会挂掉。专门测试会捕捉到很多 bugs，但并没有能力去捕捉到更多的狡猾的 bugs。相对而言，作者现在还没找到一个正确性的 bug 是线性一致性测试不能抓住的。

1. 形式方法能够保证一个分布式系统的正确性。例如，UM PLSE 研究小组最近使用 Coq proof assistnt 来验证了 Raft 一致性协议。但不幸的的是，验证需要特定的知识，另外验证实际的系统需要做大量的工作。没准有一天，验证能被用在实际系统上面，但现在，主要还是测试，而不是验证。
2. 理论上，所有的生产系统都会有一个形式规范，而且一些系统也已经有了，譬如 Raft 就有一个用 TLA+ 写的形式规范。但不幸的是，大部分的系统是没有的。