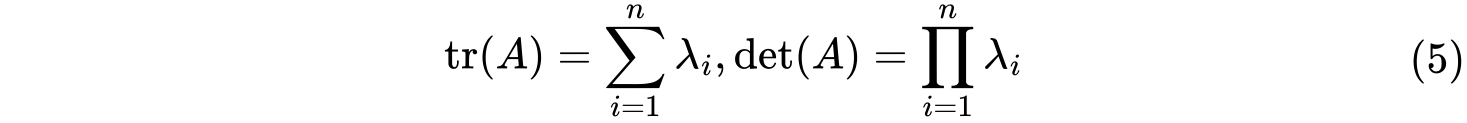【矩阵论】Chapter 4—特征值和特征向量知识点总结复习

1 特征值和特征向量

• 定义

  设$\sigma$为数域$F$上线性空间$V$上的一个线性变换，一个非零向量$v\in V$，如果存在一个$\lambda \in F$使得$\sigma(v)=\lambda v$，则$\lambda$称为$\sigma$的特征值。$\sigma$的特征值的集合称为$\sigma$的谱。并称$v$为$\sigma$的属于（或对应于）特征值$\lambda $的特征向量。

• 特征值和特征向量的求法

  设$V$是数域$F$上的$n$维线性空间，$v_1,\cdots,v_n$是$V$的一组基，线性变换$\sigma$在这组基下的矩阵为$A$，如果$\lambda$是$\sigma$的特征值，$\alpha$是相应的特征向量。则 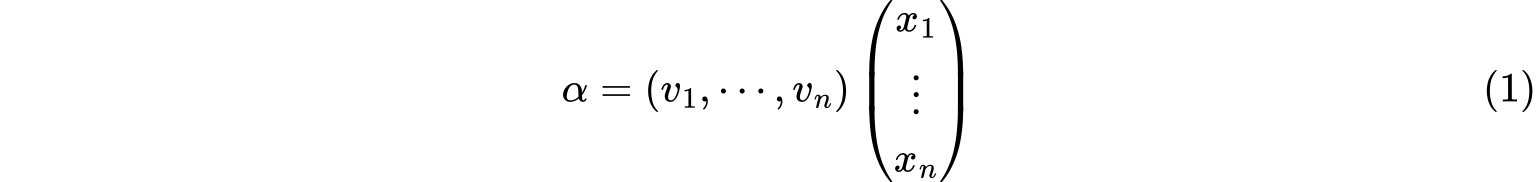将上式代入$\sigma(v)=\lambda v$得到 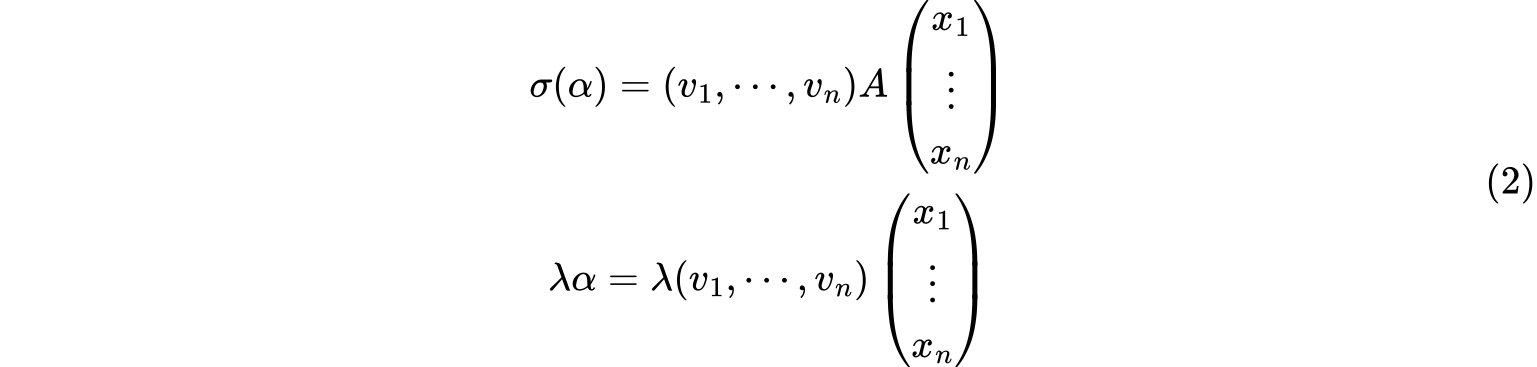由于$v_1,\cdots,v_n$线性无关，所以 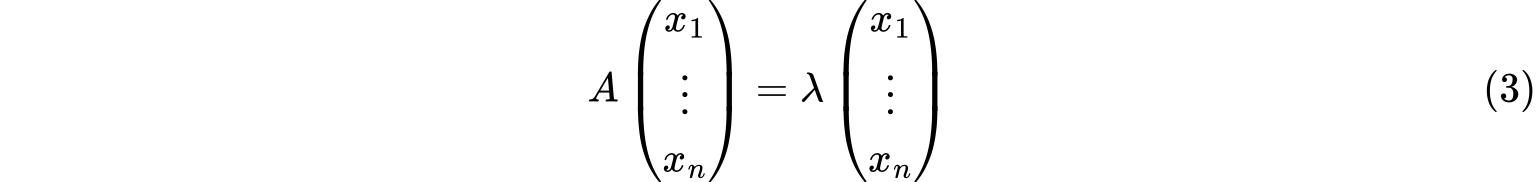则说明特征向量$\alpha$的坐标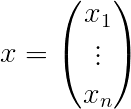满足齐次线性方程组$(\lambda I-A)x=0$。

  因为$\alpha\neq 0$，则$x\neq 0$，即齐次线性方程组$(\lambda I-A)x=0$有非零解。有非零解的充要条件是它的系数矩阵它的系数矩阵行列式$|\lambda I-A|=0$。

• 相关定义

  设$A$是数域$F$上的$n$阶矩阵，$\lambda$是一个符号，也是未知的特征值，矩阵$\lambda I-A$称为$A$的特征矩阵，其行列式$|\lambda I-A|$称为$A$的特征多项式。方程$|\lambda I-A|=0$称为$A$的特征方程，它的根（即$\lambda$的值）称为$A$的特征根（或特征值）。以$A$的特征值$\lambda$代入$Ax=\lambda x$中所得到的非零解$x$称为$A$对应于$\lambda$的特征向量。

• 定理

  设$A$为$n\times n$矩阵，$\lambda$是一个数值，以下命题等价：

  1. $\lambda$是$A$的特征值
  2. $(\lambda I-A)x=0$有一个非平凡的解（即有非零向量的解）
  3. $N(\lambda I-A)\neq{0}$
  4. $\lambda I-A$矩阵是奇异矩阵
  5. $\det(\lambda I-A)=0$

• 特征多项式的系数

  如果 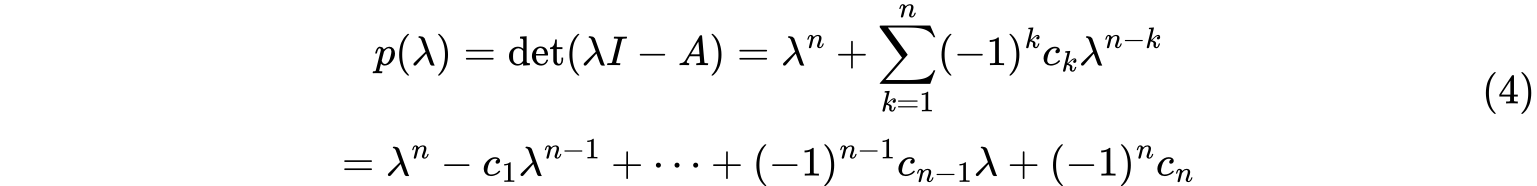则$c_k(1\leq k\leq n)$是所有$k$阶主子式（选择$k$行$k$列形成的行列式）的和，特别的，$c_1=\text{tr}(A),c_n=\text{det}(A)$。

• 定理

  1. 设$A\in C^{n\times n}$，如果$A$有特征值$\lambda_1,\cdots,\lambda_n$，则

  2. 如果$A$相似$B$，则两个矩阵有相同的特征值和特征多项式。

  3. 设$A\in C^{m\times n}$，则$A^HA$和$AA^H$特征值都是非负实数，且它们都有相同的非零特征值和相同的重数，并且非零特征值（包含重数）的数量等于$\text{rank}(A)$。

2 对角化

• 定义

  设矩阵$A\in F^{n\times n}$，如果存在一个非奇异矩阵$P\in F^{n\times n}$和一个对角矩阵$D\in F^{n\times n}$，使得$P^{-1}AP=D$，则称$A$可被对角化。

• 定理

  1. $A$可以被对角化当且仅当$A$有$n$个线性无关的特征向量
  2. $\lambda_1,\cdots,\lambda_k$是$A$的不同的特征值，则对应的特征向量$x_1,\cdots,x_k$它们是线性无关的
  3. 由以上两条定理即可推出如果$A$有$n$个不同的特征值，则$A$可被对角化
  4. 不同特征值对应的特征向量的集合的并集是线性无关的。即取每个特征值的所有特征向量，无论这些向量属于哪个特征值，它们的并集都是线性无关的。

• 代数重数

  设$A\in F^{n\times n}$，如果$\det(\lambda I-A)=(\lambda -\lambda_i)^{r_1}\cdots(\lambda-\lambda_k)^{r_k}$，其中$\lambda_1,\cdots,\lambda_k$是$A$的特征值，它们是不同的。则特征值$\lambda_i$的代数重数是$r_i$，即特征值$\lambda_i$出现的次数。

• 几何重数

  与特征值$\lambda_i$对应的特征子空间是$N(\lambda_i I-A)$，则特征值$\lambda_i$的几何重数为$\dim(N(\lambda_i I-A))$。

  几何重数$\leq $代数重数

• 几何重数看可对角化

  矩阵$A\in F^{n\times n}$可对角化当且仅当$A$中不同特征值的几何重数和等于$n$（即每个特征值的代数重数都要等于几何重数）

3 Schur定理和正规矩阵

• 酉（正交）相似定义

  设$A\in C^{n\times n}(R^{n\times n})$，如果存在一个酉（正交）矩阵$U$使得$U^HAU=B\space\space\space(U^H=U^{-1})$，则可称$A$酉（正交）相似$B$

• Schur定理

  $\forall A\in C^{n\times n}$，$A$都与上三角矩阵相似，且存在酉矩阵$U$和上三角矩阵$T$使得$U^HAU=U^{-1}AU=T$。

  仅适用于复数域，实数域上不一定适用

• 正规矩阵定义

  设$A\in C^{n\times n}$，如果$A$满足$A^HA=AA^H$，则称$A$是正规矩阵。

  Hermite矩阵，酉（正交）矩阵都是正规矩阵

• 谱定理

  设$A\in C^{n\times n}$，如果$A$是Hermite矩阵，则$A$酉相似于一个实对角矩阵，换句话说，Hermite矩阵的特征值都是实数。

• 引理

  设$A\in C^{n\times n}$，$A$是正规矩阵当且仅当$\forall \lambda,x$使得$||Ax-\lambda x||=||A^Hx-\bar{\lambda}x||$。

• 同时对角化

  设$A,B$都是相同阶数的正规矩阵，则存在一个酉矩阵可以同时酉对角化$A,B$当且仅当$AB=BA$

4 Python求解

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

import numpy as np
from sympy import symbols, Matrix
import pprint


# 定义符号变量
lambda_ = symbols('lambda')

A = np.array([[0, 2, 1], [-2, 0, 3], [-1, -3, 0]])
A = Matrix(A)

# 求特征矩阵
characteristic_matrix = A - lambda_ * np.eye(3)
pprint.pprint("关于 lambda 的特征矩阵:")
pprint.pprint(characteristic_matrix)

# 计算特征多项式
characteristic_polynomial = A.charpoly(lambda_)
pprint.pprint("关于 lambda 的特征多项式:")
pprint.pprint(characteristic_polynomial)

# 求特征值
eigenvalues = A.eigenvals()
# 打印特征值、其代数重数、特征向量和几何重数

for k, v in eigenvalues.items():
    pprint.pprint("特征值 %s 的代数重数为 %s" % (k, v))
    pprint.pprint("特征值 %s 的几何重数为 %s" % (k, A.eigenvects()[list(eigenvalues.keys()).index(k)][1]))
    pprint.pprint("特征值 %s 的特征向量为 %s" % (k, A.eigenvects()[list(eigenvalues.keys()).index(k)][2]))
    
# 判断A是否可对角化，如果可以，打印出对角化矩阵
if A.is_diagonalizable():
    pprint.pprint("A可对角化")
    pprint.pprint("对角化矩阵为:")
    pprint.pprint(A.diagonalize()[0])

# 求A的行空间、列空间、零空间
pprint.pprint("A的行空间为:")
pprint.pprint(A.rowspace())
pprint.pprint("A的列空间为:")
pprint.pprint(A.columnspace())
pprint.pprint("A的零空间为:")
pprint.pprint(A.nullspace())