【论文阅读笔记】DeepCAD: A Deep Generative Network for Computer-Aided Design Models
1 引言
现有3D生成模型:
3D点云:大量离散的3D点组成的数据表示形式;
多边形网格:一系列相连的多边形组成的3D模型;
水平集场:使用数值函数来表示物体的边界,并根据函数值的正负来确定物体内部和外部的区域;
仅能创建3D形状的离散表示,都缺少生成3D形状设计本质的能力—绘制过程。
作者提出了一个深度生成网络DeepCAD,能够输出CAD工具(如AutoCAD)中用于构建3D形状的操作序列,这是CAD模型的“绘制”过程。
这是CAD设计的生成模型的第一个工作,挑战在于CAD设计的顺序和参数化性质。CAD模型由一系列几何操作(例如,曲线草图、拉伸、圆角、布尔、倒角)组成,每个操作由某些不规则的参数(离散或连续)控制。故以前开发的3D生成模型不适合CAD模型生成。
为了克服这些挑战,需要寻求一种能够协调CAD模型中的不规则性的表示,作者考虑最常用的CAD操作(命令),并将它们统一在一个公共结构中,该结构对其命令类型、参数和序列顺序进行编码,通过类比CAD命令序列和自然语言,作者提出了一种基于Transformer网络的自编码器,它将CAD模型嵌入到潜在空间中,然后将潜在向量解码成CAD模型。【code】
为了训练这个自编码器,作者还创建了一个新的CAD命令序列数据集,以促进未来基于学习的CAD设计的研究。【dataset】
下图是DeepCAD的生成演示。
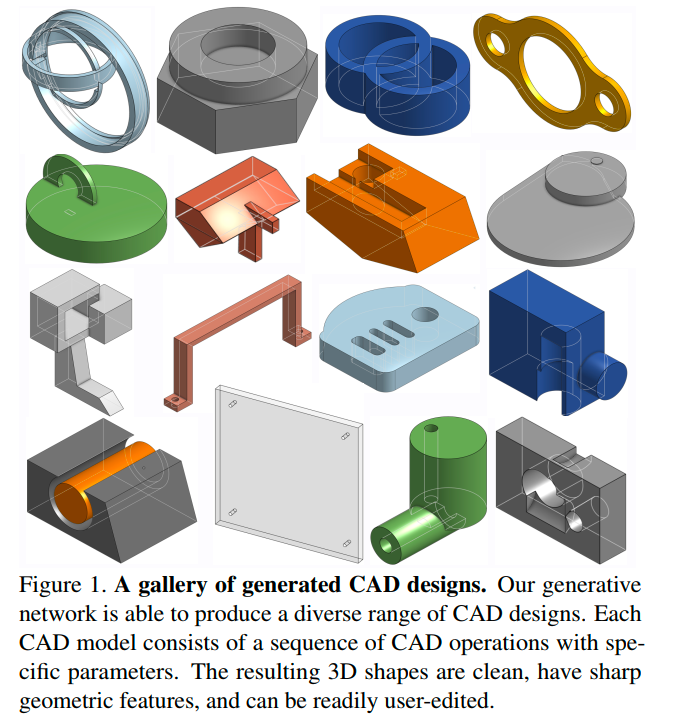
2 相关工作
参数化形状推断
深度学习的进步使得神经网络模型能够分析几何数据,推断出参数化形状。具体工作如下:
- ParSeNet:将3D点云分解为一组参数化的表面补丁。
- PIE-NET:从3D点云中提取参数化的边界曲线。
- UV-Net 和 BrepNet:专注于编码参数化模型的边界曲线和表面。
- Li等人:训练了一种神经网络,在合成数据上将2D用户草图转换为CAD操作。
- Xu等人:应用神经引导搜索,从参数化实心形状中推断出CAD建模序列。
3D形状生成模型
大多数现有方法生成离散形式的3D形状,如体素化形状、点云、多边形网格、隐式签名距离场。生成的形状可能存在噪声,缺乏锐利的几何特征,不便于用户编辑。新方法使用神经网络模型生成3D形状作为一系列几何操作。
- CSGNet:基于体素化形状输入推断CSG操作序列。
- UCSG-Net:无监督情况下推断CSG树。
- 领域特定语言(DSLs):通过DSLs合成3D形状,如ShapeAssembly。
- 作者工作:自编码器网络输出一系列CAD操作指定的CAD模型。CAD模型成为工业生产标准形状表示,可以直接导入CAD工具进行用户编辑,也可转换为点云和多边形网格。这是第一个直接生成CAD设计的生成模型。
基于Transformer的模型
Transformer网络作为基于注意力的构建模块,成功应用于自然语言处理、图像处理和其他类型数据。并行工作在约束的CAD草图生成上也依赖于Transformer网络。
与作者工作相关的还有DeepSVG-用于生成可缩放矢量图(SVG)图像的Transformer网络。SVG图像由参数化原语(如直线和曲线)描述,原语无特定顺序或依赖关系。
与SVG不同,CAD命令在3D中描述,可以是相互依赖的,必须遵循特定顺序。所以需要寻求一种新的方法在基于Transformer的自编码器中编码CAD命令及其顺序。
3 方法
DeepCAD围绕对CAD命令序列的新表示方法(3.1.2),这种CAD表示方法特别适合于输入到神经网络中。此外,这种表示法还引导出一个自然的训练目标函数(3.4)。为了训练DeepCAD,作者创建了一个新数据集,其规模远远大于同类数据集(3.3)。
3.1 神经网络的CAD表示
CAD 模型提供了两个层次的表示。
在用户交互层面,CAD 模型被描述为用户在 CAD 软件中创建实心形状时执行的一系列操作,例如用户在二维平面上绘制一个闭合曲线轮廓,然后将其拉伸成三维实心形状,再通过布尔运算等进行处理。我们将这种规范称为 CAD 命令序列。
在命令序列背后,是 CAD 模型的内核表示,广为人知的是边界表示(B-rep)。给定一个命令序列,其 B-rep 会自动计算出来,通常通过行业标准库 Parasolid。它由拓扑组件及其连接组成,以形成一个实心形状。
我们的目标是生成 CAD 命令序列的模型,而不是 B-rep。这是因为 B-rep 是命令序列的抽象:命令序列可以很容易地转换为 B-rep,但反之则很难,因为不同的命令序列可能会生成相同的 B-rep。此外,命令序列是人类可理解的,便于编辑和应用于各种下游任务。
3.1.1 CAD命令的规范
CAD 工具支持丰富的命令集,作者仅考虑了一组常用的命令,这些命令分为两类:草图和拉伸。
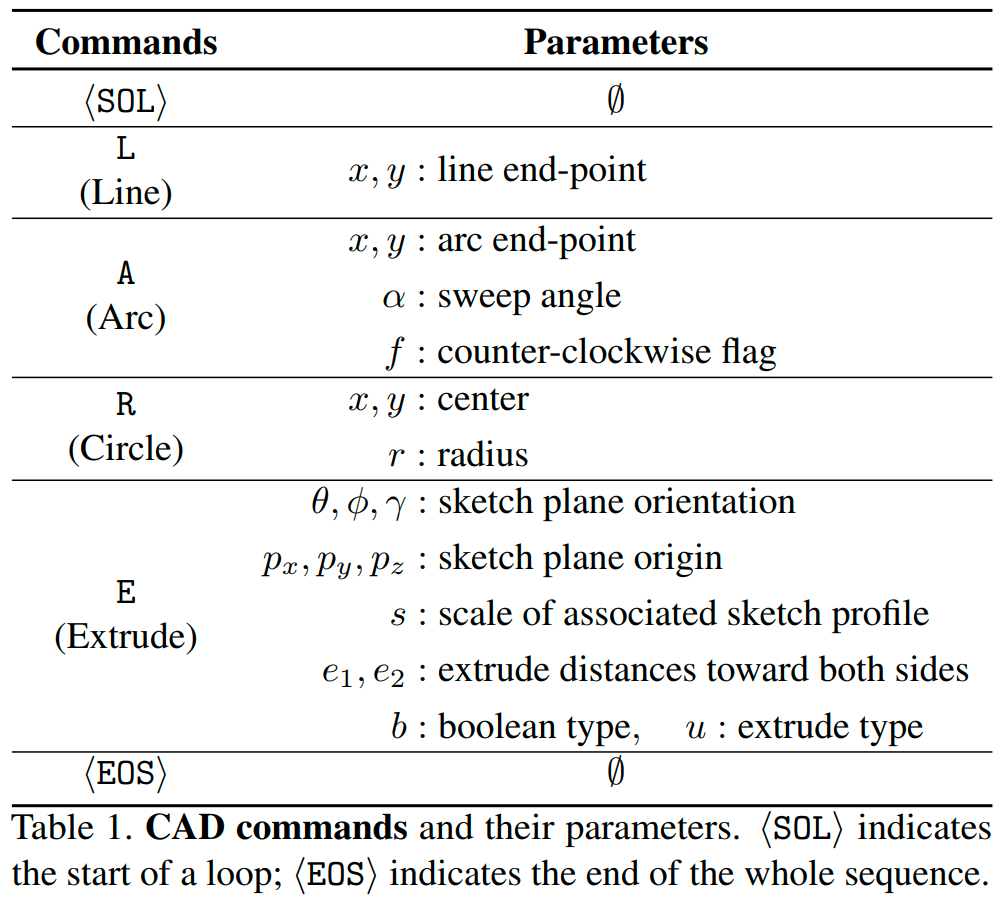
尽管概念上简单,但它们足够表达生成各种形状。
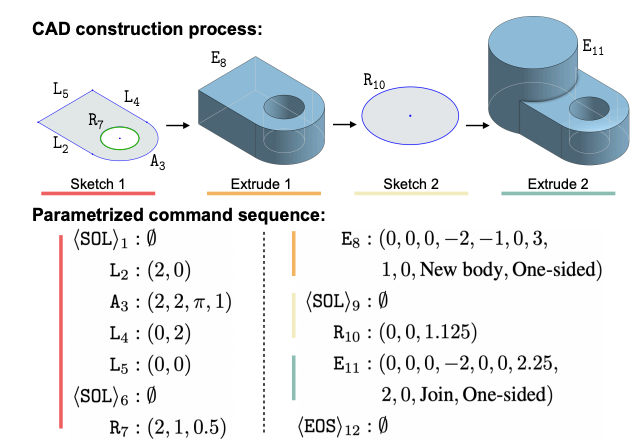
草图命令用于在三维空间中的二维平面上指定闭合曲线,每个闭合曲线称为一个环,多个环形成一个闭合区域,称为轮廓。我们的表示方法中,一个轮廓由其边界上的环列表描述(如Figure 2中的“Sketch 1”);一个环总是以指示命令开始,后跟一系列曲线命令。我们列出环上的所有曲线,并按逆时针顺序排列,开始点为最左下角的曲线。实际中,我们考虑三种最常用的曲线命令:画直线、弧线和圆。这些命令占了我们大规模现实数据集中 92% 的比例。
每个曲线命令由其曲线类型($t_i\in {\langle\text{SQL}\rangle,\text{L,A,R}}$)和参数(Table 1)描述,曲线参数指定了曲线在草图平面的局部参考框架中的二维位置。由于每个环中的曲线是一个接一个连接的,为了简洁,我们从参数列表中排除了曲线的起始位置;第一条曲线总是从草图平面的原点开始,原点的世界空间坐标在拉伸命令中指定。简言之,一个草图轮廓由一个环列表描述($S=[Q_1,\dots,Q_N]$),每个环$Q_i$由一系列从指示命令开始的曲线组成,例如$Q_i=[\langle\text{SQL}\rangle, C_1,\dots,C_{n_i}]$,每个曲线命令$C_j=(t_j,p_j)$指定曲线类型$t_j$及其形状参数$p_j$。
拉伸命令有两个目的。
它将草图轮廓从二维平面拉伸成三维实体,拉伸类型可以是单向、对称或双向。
它通过布尔运算指定如何将新拉伸的三维实体与先前创建的形状合并:创建新实体,或者与现有实体连接、切割或相交。
拉伸命令还需要定义草图平面的三维方向和其二维局部参考框架,这是通过旋转矩阵(Table 1中$(\theta,\gamma,\phi)$参数确定)定义的(为了跟平面局部参考系对齐,并将$z$轴与平面的法线方向对齐)。命令参数包括一个拉伸轮廓的比例因子$s$。
通过这些命令,我们将一个 CAD 模型$M$描述为交替出现的曲线命令和拉伸命令序列。换句话说$M=[C_1,\dots,C_{N_c}]$,其中每个$C_i=(c_i,p_i)$指定命令类型和参数。
3.1.2 网络友好的表示
我们的 CAD 模型 M 的规范类似于自然语言,词汇表由一系列 CAD 命令组成,形成句子。句子的主语是草图轮廓;谓语是拉伸。这种类比表明我们可以利用在自然语言处理中成功的网络结构(如 Transformer 网络,LLMs)来实现我们的目标。
然而,CAD 命令在几个方面与自然语言不同。每个命令有不同数量的参数。在某些命令(例如拉伸)中,参数是连续值和离散值的混合,参数值跨越不同范围。这些特性使得命令序列不适合直接用于神经网络。
为了克服这一挑战,我们对命令序列的维度进行正则化。
首先,对于每个命令,其参数堆叠成一个 $16×1$ 的向量,其元素对应于Table 1中所有命令的集合参数(例如$p_i=[x,y,\alpha,f,r,\theta,\phi,\gamma,p_x,p_y,p_z,s,e_1,e_2,b,u]$)。每个命令的未使用参数设置为 -1。
接着,我们固定每个 CAD 模型 $M$ 的命令总数 $N_c$,并通过添加空命令来填充 CAD 模型的命令序列,直到序列长度达到 $N_c$。我们选择 $N_c = 60$,这是训练数据集中出现的最大命令序列长度。
此外,我们通过量化连续参数来统一连续和离散参数。为此,我们将每个 CAD 模型规范化到一个 $2×2×2$ 的立方体内;我们还将每个草图轮廓规范化到其边界框内,并在拉伸命令中包括一个比例因子$s$来恢复规范化轮廓到其原始大小。这种规范化限制了连续参数的范围,使我们能够将其值量化为 $256$ 个级别,并使用 $8$ 位整数表示。结果是,所有命令参数都只有离散值集合。参数量化不仅是训练基于 Transformer 网络的常见实践,对于 CAD 模型来说,它对于提高生成质量尤为重要。在 CAD 设计中,必须遵循某些几何关系,例如平行和垂直的草图线条。然而,如果生成模型直接生成连续参数,通过参数回归获得的值容易产生错误,破坏这些严格的关系。相反,参数量化使网络能够将参数“分类”到特定级别,从而更好地遵循学习到的几何关系。
作者在 4.1 中通过消融研究实验证明对 CAD 命令表示选择的正确性。
3.2 CAD模型的自编码器
DeepCAD的网络架构如下:
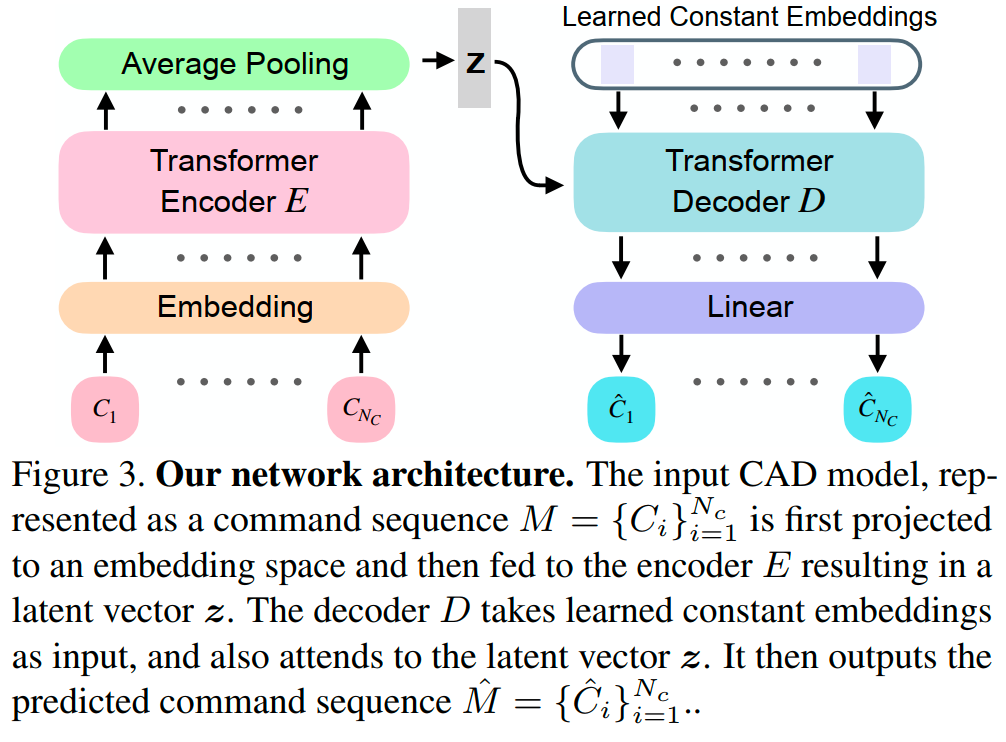
一旦训练完成,网络的解码器部分将自然地作为 CAD 生成模型。我们的自编码器基于 Transformer 网络,受其在处理序列数据方面成功的启发。自编码器输入一个 CAD 命令序列$M = [C1,\dots , C_{N_c}]$,其中 $N_c$ 是固定数量。
首先,每个命令 $C_i$ 被分别投射到维度为 $d_E = 256$ 的连续嵌入空间。然后,将所有嵌入组合起来输入编码器 $E$,输出一个潜在向量 $z\in \mathbb{R}^{256}$。解码器以潜在向量 $z$ 作为输入,输出生成的 CAD 命令序列 $\hat{M}$。
嵌入部分
与自然语言处理的方法类似,我们首先将每个命令 $C_i$ 投射到一个公共嵌入空间。然而,不同于自然语言中的词语,一个 CAD 命令 $C_i = (t_i, p_i)$ 有两个部分:命令类型 $t_i$ 和参数 $p_i$。因此,我们将 $C_i$ 的嵌入计算为三个嵌入的总和,即
$$ e(C_i) = e^\text{cmd}_i + e^{\text{param}}_i + e^\text{pos}_i\in \R^{d_E}, $$
第一个嵌入 $e^{\text{cmd}}_i$ 表示命令类型 $t_i$,由 $e^\text{cmd}_i=W_\text{cmd} \delta_i^c$ 给出。这里 $W_\text{cmd}\in\R^{d_E\times 6}$ 是一个可学习矩阵,$\delta_i^c\in \R^6$ 是一个指示命令类型 $t_i$ 的独热向量。
第二个嵌入$e^{\text{param}}_i$ 考虑命令参数。每个命令有 $16$ 个参数,每个参数被量化为一个 $8$ 位整数。我们将这些整数转换为维度为 $2^8+1=257$ 的独热向量$\delta^p_{i,j}(j=1\dots16)$,并将所有独热向量堆叠成矩阵$\delta^p_i\in\R^{257\times16}$。然后使用另一个可学习矩阵 $W_\text{param}^b\in\R^{d_E\times 257}$ 单独嵌入每个参数,并通过线性层 $W_\text{param}^a\in\R^{d_E\times 16d_E}$组合这些单独的嵌入,即
$$ e^{\text{param}}_i=W_\text{param}^a\text{flat}(W_\text{param}^b\delta^p_i), $$
其中$\text{flat}(\cdot)$将输入矩阵展平为向量
最后,位置嵌入 $e^\text{pos}_i$ 表示命令 $C_i$ 在整个命令序列中的索引,由 $e^\text{pos}_i = W_\text{pos}\delta_i$ 定义,其中 $W_\text{pos}\delta_i\in\R^{d_E\times N_c}$ 是一个可学习矩阵,$\delta_i\in\R^{N_c}$ 是一个在索引 $i$ 处填充 $1$ 其他位置填充$0$的独热向量。
编码器
编码器 $E$ 由四层 Transformer 块组成,每层有八个注意力头和 $512$ 的前馈维度。编码器将嵌入序列 $[e_1, \dots, e_{N_c}]$ 作为输入,输出向量 $[e’_1,\dots, e’_{N_c}]$,每个向量的维度为 $d_E = 256$。输出向量最终被平均以生成一个 $d_E$ 维的潜在向量 $z$。
解码器
解码器 $D$ 也建立在 Transformer 块上,具有与编码器相同的超参数设置。它以学习到的常量嵌入为输入,同时关注潜在向量 $z$。最后一个 Transformer 块的输出被送入线性层,以预测 CAD 命令序列 $\hat{M} = [ \hat{C}_1,\dots, \hat{C}_{N_c}]$,包括每个命令的命令类型 $\hat{t}_i$ 和参数 $\hat{t}_i$。与自然语言处理中常用的自回归策略不同,我们采用前馈策略,模型的预测可以分解为
$$ p(\hat{M}|z,\Theta)=\prod_{i=1}^{N_c}p(\hat{t}_i,\hat{p}_i|z,\Theta), $$
其中$\Theta$表示解码器的网络参数。
3.3 CAD数据集的创建
现有数据集:
ABC数据集:虽包含百万级别的CAD设计,但这些设计采用B-rep格式,缺乏如何通过CAD操作构建设计的具体信息;
Fusion 360 Gallery数据集:虽然提供了CAD设计及其构建指令序列,但规模仅有约8000个设计,不足以训练出泛化能力强大的生成模型。
鉴于此,作者决定创建一个全新的、大规模的数据集,该数据集不仅数量庞大,还提供了CAD命令序列,旨在满足训练自动编码网络的需求,并为未来的研究提供资源。
新数据集构建过程始于ABC数据集:
利用其中每个CAD模型链接至Onshape的原始设计。
接着,通过Onshape的FeatureScript语言(一种专门用于解析CAD操作与参数的领域特定语言),作者筛选出仅使用“草图”和“拉伸”操作的模型,舍弃了那些采用更复杂操作的模型。
对于符合条件的模型,作者编写了一段FeatureScript程序来提取其草图轮廓和拉伸操作,并将其转化为Table 1中列出的命令格式。
最终,作者收集到了总计178,238个以CAD命令序列形式描述的CAD设计,这个数量级远超现有同类型数据集。数据集进一步被随机划分为90%的训练集、5%的验证集以及5%的测试集,以备训练和测试之用。
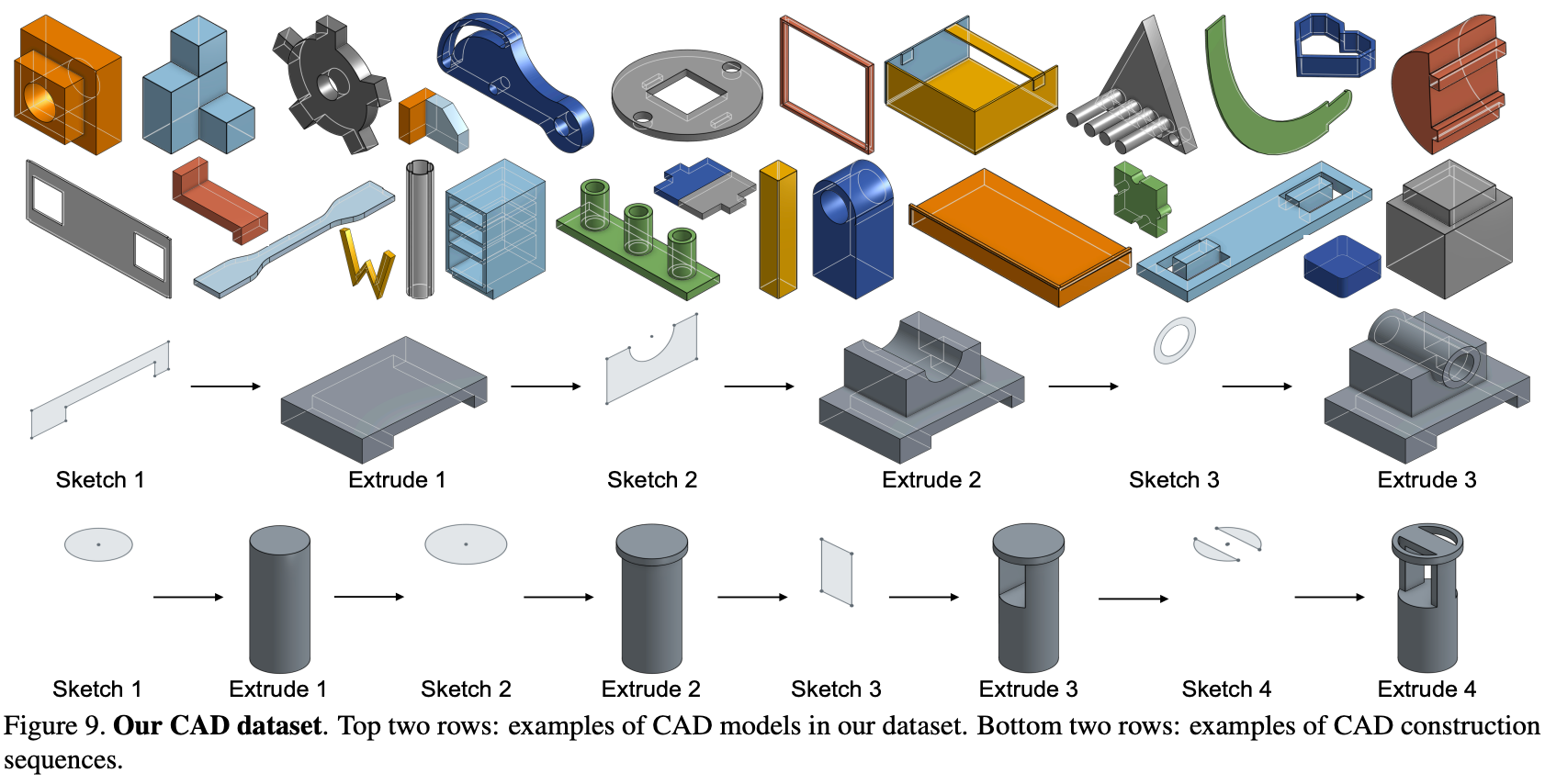
3.4 训练和运行时生成
3.4.1 训练阶段
我们利用构建的数据集对自编码器网络进行训练,采用标准的交叉熵损失函数作为优化目标。具体而言,定义预测的CAD模型$\hat{M}$与真实模型$M$之间的损失函数为:
$$ \mathcal{L} = \sum_{i=1}^{N_c} \ell(\hat{t}_i,t_i) + \beta \sum_{i=1}^{N_c} \sum_{j=1}^{N_p} \ell(\hat{p}_{i,j},p_{i,j}), $$
其中,$\mathcal{L}(·, ·)$表示标准的交叉熵损失,$N_p$每个命令的参数数量(在我们的示例中,$N_p = 16$),而$\beta$是一个权重项,用于平衡两项损失(在我们的示例中,$\beta = 2$)。值得注意的是,在真实的命令序列中,有些命令是空的(即填充命令$\langle \text{EOS} \rangle$),而有些命令参数未使用(标记为$-1$)。在这种情况下,这些元素对上述损失函数中的求和部分不做贡献。
训练过程中,我们使用Adam优化器,初始学习率为$0.001$,并设置线性预热期为前$2000$步。所有Transformer模块的Dropout率设定为$0.1$,并在反向传播中应用梯度裁剪值为$1.0$。我们以批处理大小$512$对网络进行$1000$轮的训练。
3.4.2 CAD生成阶段
当自编码器训练完成后,我们可以使用一个$256$维的潜在向量$z$来表示一个CAD模型。为了自动生成CAD模型,我们运用latent-GAN技术于已学得的潜在空间上。生成器和判别器都是简单的多层感知机(MLP)网络,各自包含四层隐藏层,它们的训练采用带有梯度惩罚的Wasserstein-GAN策略。最后,生成CAD模型时,我们从多元高斯分布中采样一个随机向量,并将其输入GAN的生成器中。GAN的输出是一个潜在向量$z$,随后将其输入基于Transformer的解码器,从而生成CAD模型。
4 实验
我们从两个角度评估我们的自编码器网络:CAD模型的自编码性能(4.1)和潜在空间形状生成(4.2)。我们还讨论了可以受益于CAD生成模型的潜在应用(4.3)。由于之前没有针对CAD设计的生成模型,因此无法直接进行比较。我们的目标是通过一系列消融实验理解模型在不同指标下的性能,并验证我们的算法选择。
4.0.3 CAD模型的自编码
自编码性能通常用于指示生成模型表达目标数据分布的程度。我们使用自编码器网络对训练数据集中不存在的CAD模型$M$进行编码,然后将所得的潜在向量解码成CAD模型$\hat{M}$。通过比较$M$和$\hat{M}$的差异来评估自编码器的性能。
指标
命令准确率($\text{ACC}_{\text{cmd}}$):衡量预测的CAD命令类型的正确性;
$$ \text{ACC}_{\text{cmd}}=\frac{1}{N_c} \sum_{t=1}^{N_c}\mathbb{I}[t_i=\hat{t_i}] , $$
参数准确率($\text{ACC}_\text{param}$):衡量命令参数的正确性;
$$ \text{ACC}_\text{param} = \frac{1}{K} \sum_{i=1}^{N_c} \sum_{j=1}^{\left| \hat{p}_i \right|} \mathbb{I}[|p_{i,j} - \hat{p}_{i,j}| < \eta]\mathbb{I}[t_i = \hat{t}_i], $$
其中$K=\sum_{i=1}^{N_c}\mathbb{I}[t_i=\hat{t}_i]|p_i|$是所有正确恢复命令中的参数总数。注意$p_{i,j}$和$\hat{p}_{i,j}$都被量化为$8$位整数,选择$\eta$是作为考虑参数量化的容差阈值,在实践中,我们选择了$\eta=3$(256个级别)
此外,我们使用Chamfer距离(CD)来评估3D几何体的质量,通过均匀采样2000个点来计算参考形状和生成形状之间的CD。另外,我们还报告无效率,即无法转换为点云的输出CAD模型的百分比。
比较方法
由于缺乏现有的CAD生成模型,我们比较了几种模型变体以验证我们的数据表示和训练策略。具体包括以下几种变体:Alt-Rel、Alt-Trans、Alt-ArcMid、Alt-Regr和Ours+Aug。每种变体在数据表示或训练策略上有所不同。
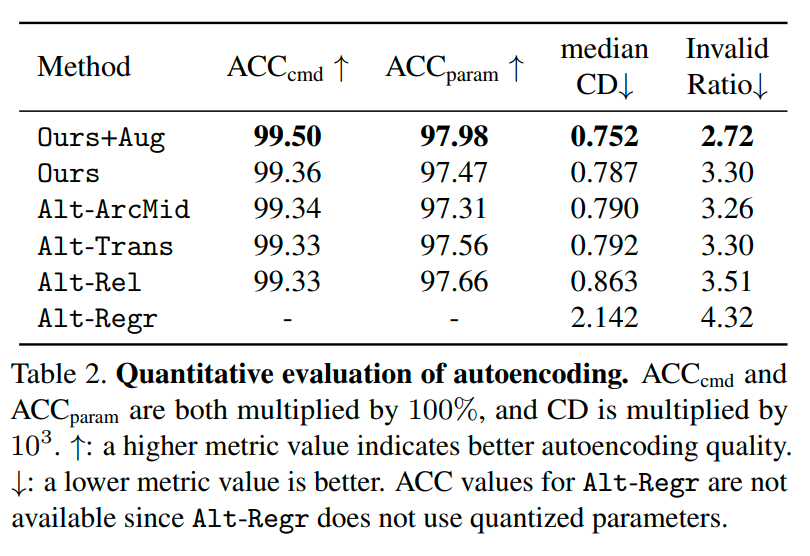
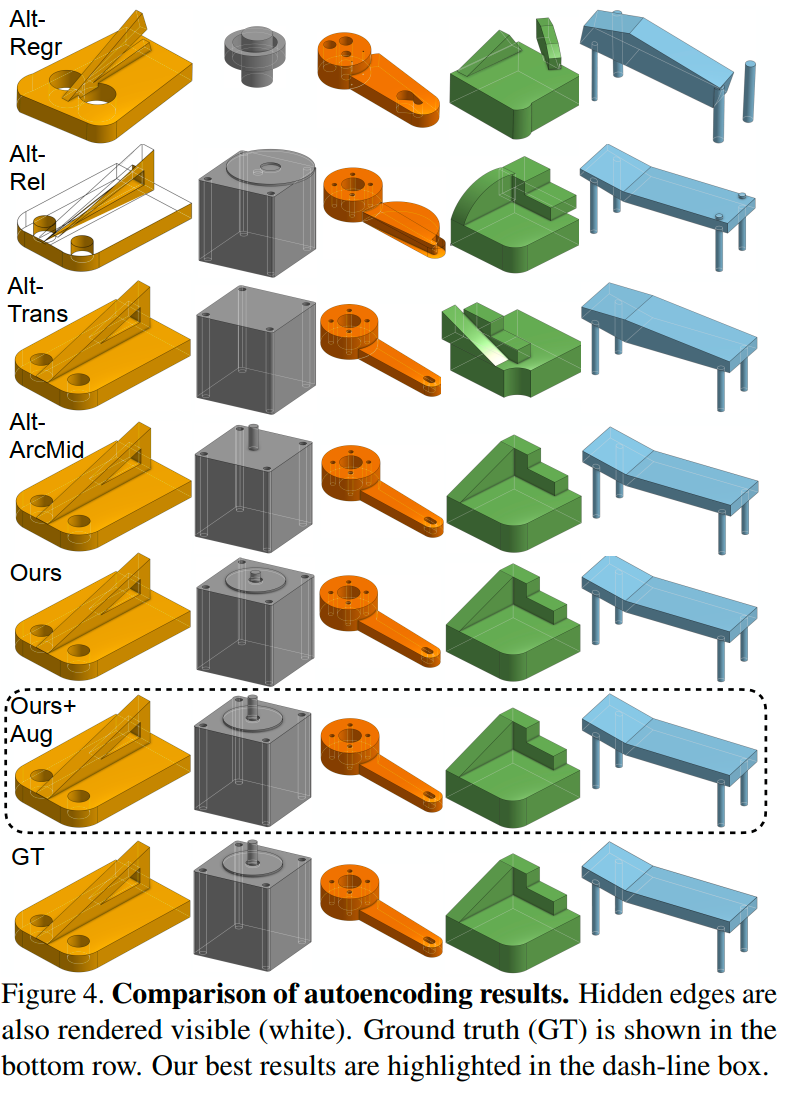
总体而言,Ours+Aug(即使用合成数据增强训练)表现最佳,表明随机组合数据可以提高网络的泛化能力。Alt-ArcMid的性能与Ours相似,说明中点表示法是表示弧的可行替代方法。Alt-Trans在CD方面略逊于Ours。虽然Alt-Rel的参数准确率(ACCparam)高于Ours,但其CD分数较大且有时会出现无效拓扑,例如在Figure 4中第二行中的黄色模型有两个三角形环路相互相交,导致拓扑无效,这是由于预测曲线位置的误差累积导致的。Alt-Regr由于不量化连续参数,误差较大,可能破坏关键的几何关系,如平行边和垂直边,例如Figure 4中的第一行。
我们还验证了我们自编码器的泛化,在其他更小的数据集(来自Autodesk Fusion 360)上评估它表现出良好的泛化能力,实现了可比较的定量性能。
4.1 形状生成
由于CAD设计没有现成的生成模型,我们选择将我们的模型与l-GAN进行比较,l-GAN是一种被广泛研究的点云三维形状生成模型。我们注意到,我们的目标并不是要显示出孰优孰劣,因为这两种生成模型有不同的应用领域。相反,我们证明了我们的模型即使在点云生成模型的度量下也能产生可比的形状质量。

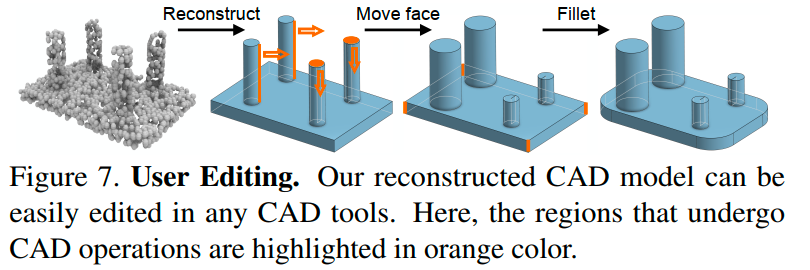
此外,如Figure 5所示,我们模型中的形状具有更清晰的几何细节,并且可以轻松地进行用户编辑(Figure 7)。
为了与点云生成模型进行定量比较,我们遵循l-GAN中使用的指标。这些度量标准用于衡量两组3D点云形状之间的差异,即真实形状集合$S$和生成形状集合$G$。
覆盖率(COV):衡量$S$中的形状有多少可以很好地近似为G中的形状;
最小匹配距离(MMD):表示$S$和$G$中两个点云之间的最小匹配距离来衡量$G$的保真度;
Jensen-Shannon散度(JSD):衡量$S$和$G$的点云分布的相似性
然后,我们将真实和生成的CAD模型转换为点云,并评估这些度量标准。结果如下:
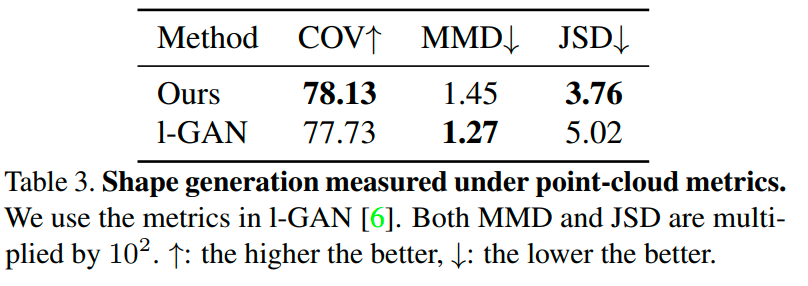
表明我们的方法在点云度量标准方面与l-GAN具有可比性的性能。然而,由于其参数化表示,CAD模型具有比点云更平滑的表面和更锐利的几何特征。
4.2 未来应用
借助CAD生成模型,可以将点云(例如通过3D扫描获取的)重建为CAD模型,例如作者这里使用自编码器将CAD模型$M$编码为潜在向量$c$。然后,利用PointNet++编码器训练它将$M$的点云表示编码为相同的潜在向量$c$。在推断时,给定一个点云,我们使用PointNet++编码器将其映射到潜在向量,然后使用我们的自编码器解码为CAD模型。
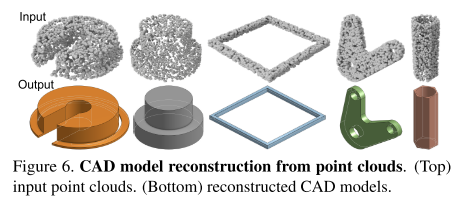
生成的CAD模型可以直接导入CAD工具进行用户编辑。
5 总结
作者提出了DeepCAD,第一个一个用于CAD设计的深度生成模型。几乎所有以前的3D生成模型都产生离散的3D形状,如体素、点云和网格。为此,作者还引入了一个大型CAD模型数据集,每个模型都表示为一个CAD命令序列。
在构建CAD生成模型的过程中,作者的方法存在以下几个主要限制:
曲线命令类型有限:目前,作者仅考虑了三种最常用的曲线命令类型(直线、弧线和圆)。然而,其他曲线命令也可以轻松添加,例如可以通过三个控制点以及起点来指定的三次贝塞尔曲线,其参数结构可以按照3.1中描述的方式进行。
操作命令的局限性:虽然像旋转草图这样的操作可以类似于拉伸命令进行编码,但某些CAD操作(如倒角)作用于形状边界的部分,因此需要参考模型的B-rep(边界表示),而不仅仅是其他命令。将这些命令纳入生成模型仍需进一步研究。
拓扑有效性无法保证:并非每个CAD命令序列都能生成拓扑上有效的形状。作者的生成网络不能保证其输出的CAD序列的拓扑一致性。在实践中,生成的CAD命令序列很少失败,但随着命令序列变长,失败的可能性增加。
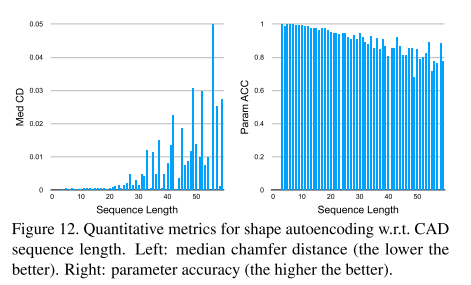
相关内容
 支付宝
支付宝 微信
微信