$\lambda$矩阵与Jordan 标准型

1 $\lambda $矩阵关键概念

• $\lambda$矩阵定义

  设$a_{ij}(\lambda)(1\leq i \leq m,1\leq j \leq n)$是数域$P$上的多项式，以$a_{ij}(\lambda)$为元素的$m\times n$矩阵 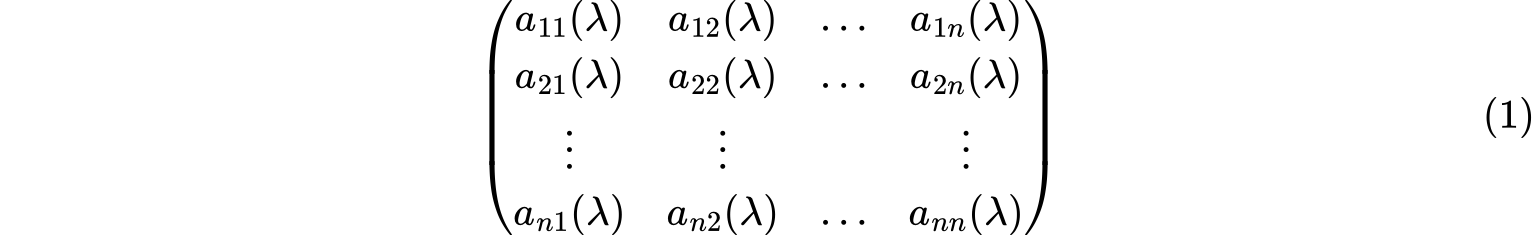成为多项式矩阵或$\lambda$矩阵，多项式$a_{ij}(\lambda)(1\leq i \leq m,1\leq j \leq n)$中的最高次数成为$A(\lambda)$的次数，则数字矩阵显然是$\lambda$矩阵，为$0$次；数字矩阵$A$的特征矩阵$\lambda I-A$就是$1$次$\lambda$矩阵。

  设$A(\lambda)$矩阵的次数为$k$，则$A(\lambda)$可表示为 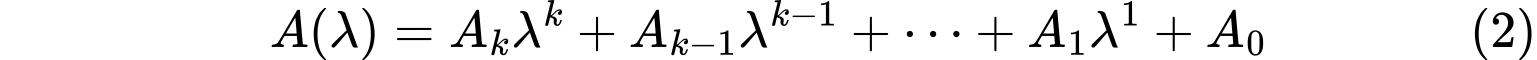其中$A_i(0\leq i \leq k)$是数字矩阵，并且$A_k\neq 0$。

• $\lambda$矩阵性质

  1. $\lambda$矩阵也可以进行初等变换
  2. 若$A(\lambda)$可以经过有限次初等变换化为$B(\lambda)$，则称$\lambda$矩阵$A(\lambda)$和$B(\lambda)$相抵，记为$A(\lambda)\cong B(\lambda)$

• $\lambda$矩阵定理

  设$A(\lambda)=(a_{ij}(\lambda))\in P[\lambda]^{m\times n}$，且$rank(A(\lambda))=r$，则$A(\lambda)$相似于如下的对角矩阵 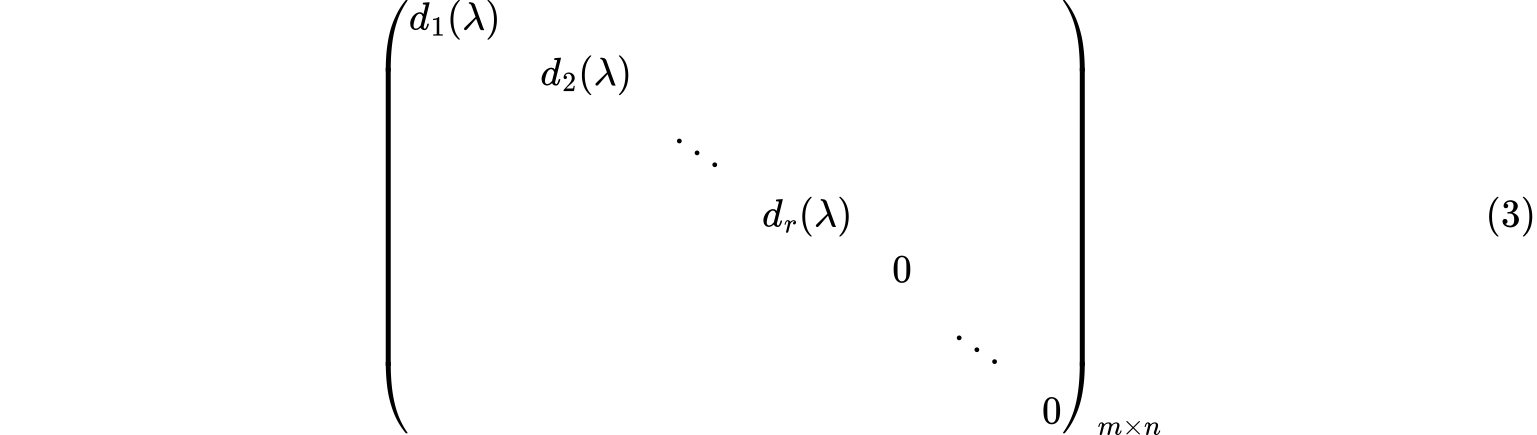其中$d_i(\lambda)(1\leq i \leq r)$是首项系数为$1$的多项式，并且$d_i(\lambda)|d_{i+1}(\lambda)(1\leq i \leq r-1)$

• $Smith$标准型

  $\lambda$矩阵定理中的对角矩阵就称为$\lambda $矩阵$A(\lambda)$在相抵下的标准型或者$Smith$标准型。

  $Smith$标准型是唯一的

• 不变因子、行列式因子、初等因子

  重要性质：相抵的$\lambda$矩阵具有相同的秩、相同的各阶行列式因子、相同的不变因子

  $Smith$标准型“主对角线”上非零元$d_1(\lambda),d_2(\lambda),\dots,d_r(\lambda)$称为$A(\lambda)$的不变因子；

  $A(\lambda)$的全部$k$阶子式的最大公因式称为$A(\lambda)$的$k$阶行列式因子，记为$D_k(\lambda)$；

  其中$d_k(\lambda)=\frac{D_{k+1}(\lambda)}{D_k(\lambda)}$

  初等因子是从不变因子分解得来的，具体如下：

  假设不变因子为 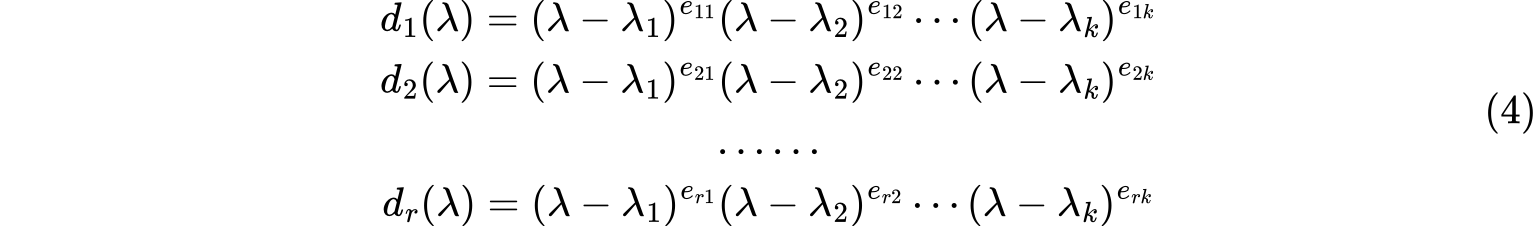则所有指数大于$0$的因子$(\lambda -\lambda _ {j})^ {e_ {ij}}(1\leq i \leq r,1\leq j\leq k)$称为$\lambda $矩阵$A(\lambda)$的初等因子

2 矩阵相似的条件

• 定义

  设$A$为$n$阶数字矩阵，其特征矩阵$\lambda I-A$的行列式因子，不变因子和初等因子分别称为矩阵$A$的行列式因子，不变因子和初等因子。

• 相似的充分必要条件

  $n$阶矩阵$A$和$B$相似$\Longleftrightarrow $存在一个可逆矩阵 $P$，使得$B = P^{-1} A P $$\Longleftrightarrow $它们的特征矩阵$\lambda I-A$和$\lambda I-B$相抵$\Longleftrightarrow $它们具有相同的行列式因子或者它们有相同的不变因子$\Longleftrightarrow $它们具有相同的初等因子

3 矩阵的Jordan标准型

• Jordan块和Jordan标准型

  Jordan块分上Jordan块和下Jordan块，我们一般用上Jordan块。

  如果$(\lambda -a)^d$是$A$的初等因子，我们则可以构建一个$d\times d$的矩阵形式 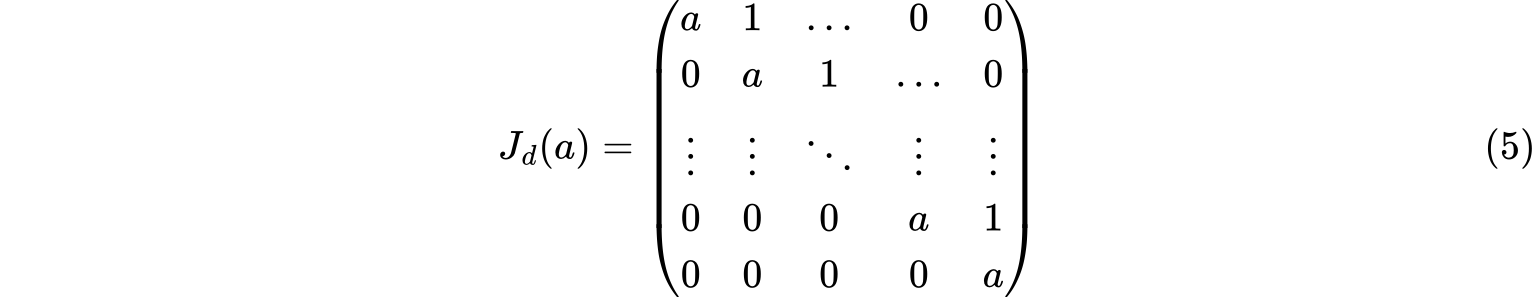这个矩阵我们称为上Jordan块。下Jordan块则为 那由若干个Jordan块为对角块组成的块对角矩阵称为Jordan标准型

• 性质

  1. Jordan块被它的初等因子唯一确定
  2. Jordan标准型的全部初等因子由它的全部Jordan块的初等因子组成
  3. 每个$n$阶矩阵都相似于它的Jordan标准型
  4. Jordan标准型不唯一，其内部Jordan块的顺序可以随意，但每个Jordan块唯一，如果除去其中Jordan块排列的次序外是被矩阵$A$唯一确定的

• 求$n$阶方阵$A$的Jordan标准型

  1. 得到$(\lambda I-A)$矩阵，求它的各阶行列式因子$D_k(\lambda)$
  2. 根据公式$d_1(\lambda)=D_1(\lambda)$，$d_k(\lambda)=\frac{D_{k+1}(\lambda)}{D_k(\lambda)}(2\leq k\leq n)$得到不变因子
  3. 从不变因子分解得到初等因子
  4. 根据初等因子构成Jordan块$J_i$，再组成Jordan标准型$J$

• 求可逆矩阵$P$，使得$P^{-1}AP=J$

  1. 根据上一个方法求出矩阵$A$的Jordan标准型$J$

  2. 左右两边左乘$P^{-1}$变换公式得到$AP=PJ$

  3. 设$P=(P_1,..,P_n)$，根据公式构造 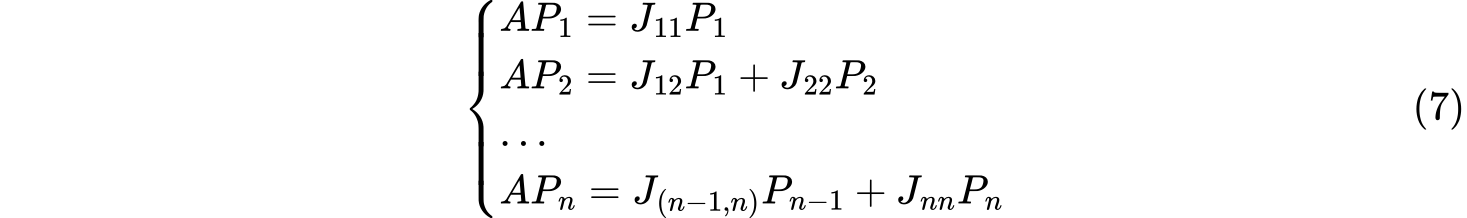其中$J_{(i,i+1)}$的取值只能为$0\space or\space 1$，$J_{ii}$的取值即为对角线元素。根据方程从而解得$P$。

  注意：$P$不唯一，但是我们在设$P$元素的时候一定要保证$P$可逆，即$rank(P)=n$。可以自己进行初等变换验证一下是否正确！

• Python求解$J$和可逆矩阵$P$

  1 2 3 4 5 6 7 8 9 10 11

  import numpy as np from sympy import Matrix import pprint A = np.array([[2, 2, 1], [-2, 6, 1], [0, 0, 4]]) A = Matrix(A) P, J = A.jordan_form() # 验证P^-1 * A * P = J assert P ** -1 * A * P == J, "P^-1 * A * P != J" pprint.pprint("P:", P) pprint.pprint("J:", J)

4 Cayley-Hamilton 定理与最小多项式

• Cayley-Hamilton 定理

  设$A$是$n$阶矩阵，$f(\lambda)$是$A$的特征多项式，则$f(A)=0$

• 相关定义

  设$A$为$n$阶矩阵，如果存在多项式$\varphi(\lambda)$使得$\varphi(A)=0$，则称$\varphi(\lambda)$为$A$的化零多项式。易知$f(\lambda)$为$A$的化零多项式，且$g(\lambda)f(\lambda)$也为$A$的化零多项式，故$A$的化零多项式有无穷多个

  $A$的所有化零多项式中，次数最低，且首项系数为$1$的多项式称为$A$的最小多项式。$A$的最小多项式是唯一的

• 结论

  $A$的最小多项式就是$d_n(\lambda)$，即$A$的第$n$个不变因子