比例份额调度

在本章中，我们将研究一种不同类型的调度器，称为比例份额（Proportional-share）调度器，有时也称为公平共享调度器。比例共享基于一个简单的概念：调度器可能会尝试保证每个作业获得一定百分比的 CPU 时间，而不是针对周转时间或响应时间进行优化。

比例份额调度有一个非常出色的早期例子是彩票调度（lottery scheduling），由 Waldspurger 和 Weihl 发现。其基本思想非常简单，每隔一段时间，就会举行一次彩票抽奖，来确定接下来该运行哪个进程。更频繁运行的进程则更有机会中奖。

在处理细节前先抛出我们的关键问题：如何按比例共享CPU？我们如何设计一个调度器以按比例共享 CPU？这样做的关键机制是什么？它们的效果如何？

1 基本概念：彩票代表份额

彩票调度背后是一个非常基本的概念：彩票数，代表了进程（或用户或其他）占有某个资源的份额。一个一个进程拥有的彩票数占总彩票数的百分比，就是它占有系统资源的份额。

例如，有两个进程A和B，其中A有75张彩票，而B只有25张彩票。因此，我们希望A占有$75%$的CPU，B占有$25%$的CPU。

彩票调度通过每隔一段时间（比如每个时间片）举行一次抽奖，以概率方式（而非确定方式）实现这一目标。举行抽奖很简单：调度器必须知道总共有多少张彩票（在我们的例子中，有 100 张彩票），调度器接下来随机抽取中奖彩票，是$[0,99]$的数字。假设 A 持有 0 到 74 号彩票，B 持有 75 到 99 号彩票，中奖彩票就决定了运行A或B。然后调度程序加载中奖进程的状态，并运行它。

下面是彩票调度程序输出的中奖彩票和对应的调度结果:

从这个例子中我们可以看出，彩票调度的随机性导致了从概率上满足期望的比例，但不能确保。在上面的例子中，工作 B 运行了 20 个时间片中的 4 个，只是占了$20%$，而不是期望的$25%$。但是，这两个工作运行得时间越长，它们得到的 CPU 时间比例就会越接近期望。

随机性决策有优势也有劣势：

• 优势
  1. 避免最差情况
  2. 轻量，不需要记录过多状态，传统公平调度需要记录进程的大量状态
  3. 随机方法很快，决策也快
• 劣势
  1. 系统行为可能不可预测，因为它们不受先前状态或输入的直接影响，这可能导致一些进程等待时间过长，而另一些则过短。
  2. 可能导致性能波动

TIP：使用彩票数代表份额

彩票（和步幅）调度设计中最强大（也是基本）的机制之一就是彩票数机制。在这些示例中，彩票数用于表示进程对 CPU 的份额，但其应用范围可以更广泛。例如，在虚拟机管理程序虚拟内存管理的最新研究中，Waldspurger 展示了如何使用彩票数来表示客户操作系统的内存份额。因此，如果您需要一种机制来代表一定比例的所有权，这个概念可能就是……（等等）……彩票数。

2 彩票机制

彩票调度还提供了许多机制，以不同的方式（有时是有用的方式）操纵彩票。一种机制是彩票货币（ticket currency）。这种机制允许拥有一组彩票的用户在自己的工作中以任意货币分配彩票；然后系统会自动将所述货币转换为正确的全局彩票。

例如，假设用户A和用户B都有100张彩票，A正在运行两个作业：A1和A2，然后用 A 的货币给它们每人 500 张彩票（总共 1000 张）。用户B正在运行一个作业，然后用B的货币给它分配10张彩票（总共10张）。系统将 A1 和 A2 的分配从 A 货币各 500 转换为全球货币各 50；同样，B1的10张票折算为100张票。然后在全球彩票货币（共 200 个）上进行抽签，以决定哪个工作运行。A1的具体计算方法是$\frac{\text{Ticket}{A1}}{\text{Ticket}{A1}+\text{Ticket}{A2}}\times \text{Ticket}{A}$，其他同理。

1
2
3
4
5
6
7
8
9

User A

-> 500 (A's ticket currency) to A1 -> 50 (global currency)

-> 500 (A's ticket currency) to A2 -> 50 (global currency)

User B

-> 10 (B's ticket currency) to B1 -> 100 (global currency)

另一个有用的机制是彩票转让（ticket transfer）。通过转让，一个进程可以暂时将其彩票转让给另一个进程。这种能力在客户端/服务器设置中特别有用，其中客户端进程向服务器发送消息，要求服务器代表客户端执行一些工作。为了加快工作速度，客户端可以将彩票转让给服务器，并尝试最大化服务器的性能，同时处理客户端的请求。完成后，服务器将票据归还给客户端，一切如旧。

最后，彩票通胀（ticket inflation）机制有时也很有用。通过通货膨胀，进程可以暂时增加或减少其拥有的彩票数。当然，在进程相互不信任的竞争场景中，这是没有意义的；一个贪婪的进程可以给自己大量的彩票从而接管机器。但是，通胀可以应用于一组进程相互信任的环境中。在这种情况下，如果任何一个进程知道它需要更多的 CPU 时间，它可以增加自己的彩票数，作为向系统反映该需求的一种方式，而无需与任何其他进程进行通信。

3 实现

彩票调度最令人惊叹的地方可能就是其实施的简单性。你只需要一个好的随机数生成器来挑选中奖彩票，一个跟踪系统进程的数据结构（如列表），以及彩票总数。

假设我们将进程保存在一个列表中。下面是一个由 A、B 和 C 三个进程组成的示例，每个进程都有一定数量的彩票数。

为了做出调度决策，我们首先要从门票总数（400） 中随机抽取一个数字（中奖号码）。然后，我们只需遍历列表，用一个简单的计数器帮助我们找到中奖者。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

# counter: used to track if we've found the winner yet
counter = 0

# winner: use some call to a random number generator to get a value, between 0 and the total # of tickets
winner = random.randint(0, totaltickets)

# current: use this to walk through the list of jobs
current = head

# loop until the sum of ticket values is > the winner
while current:
    counter = counter + current.tickets
    if counter > winner:
        break  # found the winner
    current = current.next

# 'current' is the winner: schedule it...

该代码从前往后遍历进程列表，将每个彩票值添加到计数器中，直到该值超过获胜者。一旦出现这种情况，当前列表进程就是中奖者。以中奖彩票为 300 的示例为例，会发生以下情况。首先，计数器增加到 100 以计算 A 的票；因为 100 小于 300，所以循环继续。然后计数器会更新为 150（B 的票），仍然少于 300，因此我们再次继续。最后，计数器更新为 400（明显大于 300），因此我们跳出循环，当前指向 C（中奖者）。

要让这个过程更有效率，建议将列表项按照彩票数递减排序。这个顺序并不会影响算法的正确性，但能保证用最小的迭代次数找到需要的结点，尤其当大多彩票被少数进程掌握时。

4 评估指标

为了更容易理解动态彩票调度，我们现在对两个相互竞争的作业的完成时间进行简要研究，每个作业都有相同数量的彩票 (100) 和相同的运行时间 (R，我们将改变它) 。

在这种情况下，我们希望每个作业大致在同一时间完成，但由于彩票调度的随机性，有时一个作业会先于另一个作业完成。为了量化这种差异，我们定义了一个简单的不公平指标（unfairness metric） $U$，它就是第一个作业完成的时间除以第二个作业完成的时间。

例如，如果 R = 10，并且第一个作业在 10 完成（第二个作业在 20 完成），则 $U=\frac{10}{20}=0.5$。当两个作业几乎同时完成时，$U$ 将非常接近 1。在这种情况下，这就是我们的目标：完全公平的调度程序将实现 $U = 1$。

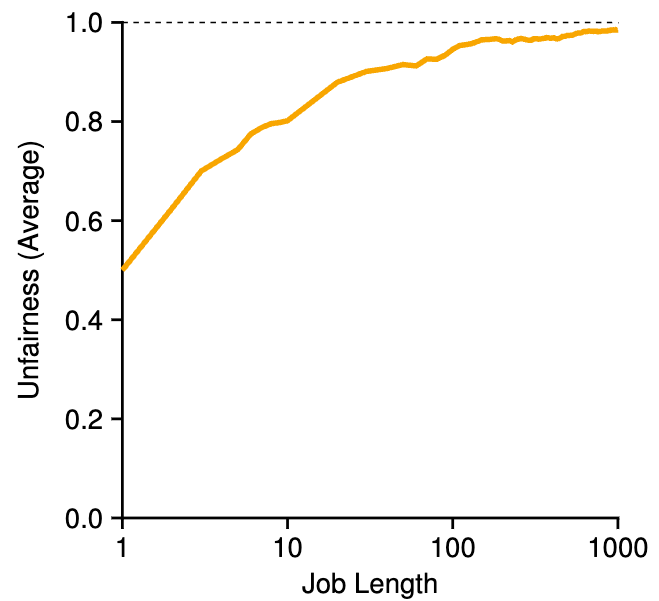
下图描绘了在30次试验中，两个作业（R）的长度从1到1000不等时的平均不公平性。从图中可以看出，当工作时间不长时，平均不公平现象可能相当严重。只有当作业运行了大量的时间片时，彩票调度程序才能接近所需的结果。

5 如何分配彩票

在彩票调度方面，我们尚未解决的一个问题是：如何为作业分配彩票？这是一个棘手的问题，因为系统如何运行当然在很大程度上取决于如何分配彩票。一种方法是假定用户最了解情况；在这种情况下，每个用户都会得到一定数量的门票，用户可以根据需要将门票分配给他们运行的任何作业。然而，这种解决方案不是解决方案：它并没有告诉你该怎么做。因此，在给定一系列工作的情况下，“彩票分配问题 “仍然悬而未决。

6 步幅调度

你可能还想知道：为什么要使用随机性呢？如上所述，虽然随机性可以为我们提供一个简单（且近似正确）的调度器，但它偶尔无法提供精确正确的比例，尤其是在短时间内。为此，Waldspurger 发明了一种确定性公平分配调度器—步幅调度器 。

步幅调度也很简单，系统中每个作业都有一个步幅，这与它拥有的彩票数成反比。在上面的示例中，对于作业 A、B 和 C，分别有 100、50 和 250 张彩票，我们可以通过将某个较大的数字除以每个进程分配的彩票数量来计算每个作业的步幅。例如，如果我们用 10,000 除以每个彩票值，我们将获得 A、B 和 C 的步幅值：100、200 和 40。我们将此值称为每个进程的步幅；每次进程运行时，我们都会按其步幅增加它的计数器（称为其行程值），以跟踪其全局进度。

然后，调度程序使用步幅和行程值来确定接下来应该运行哪个进程。基本思想很简单：在任何给定时间，选择迄今为止具有最低行程值的进程来运行；当您运行一个进程时，按其步幅增加其行程值。 Waldspurger 提供了伪代码实现：

1
2
3
4

curr = remove_min(queue); // pick client with min pass
schedule(curr); // run for quantum
curr->pass += curr->stride; // update pass using stride
insert(queue, curr); // return curr to queue

在我们的示例中，一开始有三个进程（A、B 和 C），它们的步幅分别为 100、200 和 40，所有进程的行程值最初都是 0。假设我们选择 A（任意选择；可以选择任何一个行程值同样低的进程）。A 运行后，在完成时间片后，我们将其行程值更新为 100。然后运行 B，将其行程值设置为 200。最后运行 C，其行程值递增到 40。此时，算法将选择最低的行程值，即 C的行程值，然后运行C，将其行程值更新为 80（C 的步幅为 40）。然后 C 将再次运行（仍然是最低的行程值），将其行程值提升至 120。A 现在运行，将其行程值更新为 200（现在等于 B 的行程值）。然后 C 再运行两次，将其行程值更新为 160，然后是 200。此时，所有行程值再次相等，这个过程将无限重复。下表跟踪了调度器随时间变化的行为。

从上表可以看出，C运行了5次，A2次，B只有一次，正好与它们的彩票值 250、100 和 50 成比例。彩票调度是随着时间的推移概率性地实现比例的，而步幅调度则是在每个调度周期结束时精确地实现比例。

所以你可能想知道：跨步调度这么精准，为什么还要使用彩票调度呢？嗯，彩票调度有一个步幅调度没有的好特性：没有全局状态。想象一下，在上面的跨步调度示例中，有一个新作业进入；它的行程值应该是多少？应该设置为0吗？如果是的话，就会独占CPU。对于彩票调度，每个进程没有全局状态；我们只需添加一个新进程及其拥有的任何彩票，更新单个全局变量以跟踪我们总共拥有多少彩票，然后从那里开始。通过这种方式，彩票以合理的方式合并新进程更加容易。

7 Linux完全公平调度器（CFS）

尽管在公平份额调度方面已有早期工作，但当前的Linux方法以另一种方式实现了类似的目标。名为完全公平调度器（或CFS）的调度器实施了公平份额调度，但是以高效且可扩展的方式进行。

为了实现其效率目标，CFS通过其固有设计和对任务非常适合的数据结构巧妙地使用极少时间做出调度决策。最近研究表明，调度器效率非常重要；具体而言，在对谷歌数据中心进行研究时，Kanev等人发现，即使经过积极优化，调度仍然占用整个数据中心约5%的CPU时间。因此，尽可能减少开销是现代调度程序架构的一个关键目标。

7.1 基本操作

大多数调度程序都基于固定时间片的概念，而 CFS 的运行方式则有些不同。它的目标很简单：将 CPU 公平地平均分配给所有竞争进程。它通过一种简单的基于计数的技术来实现这一目标，这种技术被称为虚拟运行时间（vruntime）。

每个进程运行时，都会累积vruntime。在最基本的情况下，每个进程的 vruntime 都以相同的速率增长，与物理（实际）时间成比例。在进行调度决策时，CFS 会选择 vruntime 最低的进程作为下一个运行进程。

那这就提出了一个问题：调度器怎么知道何时停止正在运行的进程，并运行下一个进程呢？这里矛盾就很明显：如果 CFS 切换过于频繁，公平性就会提高，因为 CFS 将确保每个进程即使在极小的时间窗口内也能获得其 CPU 份额，但代价是性能降低（上下文切换过多）；如果 CFS 切换频率降低，性能就会提高（上下文切换减少），但代价是近期公平性降低。

CFS通过各种控制参数来管理这种矛盾。第一个是sched_latency（调度延迟），CFS使用该值来确定一个进程在考虑切换之前应运行多长时间（以动态方式有效确定其时间片）。典型的sched_latency值为$48$（毫秒），CFS 将该值除以 CPU 上运行的进程数（n），以确定进程的时间片，从而确保在这段时间内，CFS 完全公平。

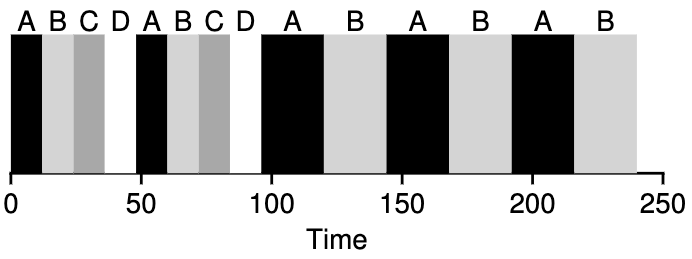
例如，如果这有$n=4$的进程在运行，CFS将sched_latency的值除以$n$得出每个进程的时间片为$12\text{ms}$。然后，CFS 会调度第一个作业并运行它，直到用完 $12\text{ms}$ 的（虚拟）运行时间，然后检查是否有 vruntime 更低的作业可替代运行。在这种情况下，如果有，CFS 就会切换到其他三个作业中的一个，依此类推。下图展示了这样一个例子：四个作业（A、B、C、D）以这种方式各运行两个时间片；其中两个作业（C、D）完成后，只剩下两个作业，然后它们以循环方式各运行 $12\text{ms}$。

但如果有 “太多 “进程在运行呢？这会不会导致时间片太小，从而导致太多的上下文切换？答案是肯定的。

为了解决这个问题，CFS增加了另一个参数min_granularity，通常设置为 6 ms。CFS绝不会设置进程的时间片小于值，确保不会在调度开销上花费太多时间。

例如，这有10个进程正在运行，我们原来的计算会用sched_latency除以$10$得出进程时间片（结果为$4.8\text{ms}$）。但因为min_granularity，CFS会每个进程的时间片设置为$6\text{ms}$。虽然 CFS 的公平性不会超过在 $4.8\text{ms}$ 的目标调度延迟（sched_latency），但它将接近目标值，同时仍能实现较高的 CPU 效率。

需要的注意是，CFS 使用的是周期性定时器中断，这意味着它只能在固定的时间间隔内做出决定。该中断会频繁响起（例如，每 1 ms响一次），让 CFS 有机会唤醒并确定当前作业是否已运行结束。如果作业的时间片不是定时器中断间隔的整数倍，也没关系；CFS 会精确跟踪 vruntime，这意味着从长远来看，它最终会接近理想的 CPU 共享状态。

7.2 权重（优先级）

CFS 还可以控制进程优先级，使用户或管理员能够为某些进程提供更高的 CPU 份额。它不是通过彩票来实现这一点，而是通过经典 UNIX 机制—进程的nice级别的来实现这一点。对于进程，nice 参数可以设置为 -20 到 +19 之间的任意值，默认值为 0。正的 Nice 值意味着较低的优先级，负值意味着较高的优先级；当你太好的时候，你就不会得到那么多（安排）关注，唉。

CFS将每个进程的nice值映射到一个权重，如下所示：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

static const int prio_to_weight[40] = {
	/* -20 */ 88761, 71755, 56483, 46273, 36291,
    /* -15 */ 29154, 23254, 18705, 14949, 11916,
    /* -10 */ 9548, 7620, 6100, 4904, 3906,
    /* -5 */ 3121, 2501, 1991, 1586, 1277,
    /* 0 */ 1024, 820, 655, 526, 423,
    /* 5 */ 335, 272, 215, 172, 137,
    /* 10 */ 110, 87, 70, 56, 45,
    /* 15 */ 36, 29, 23, 18, 15,
};

有了这些权重，我们就可以计算每个进程的有效时间片（就像我们之前所做的），但现在要考虑它们的优先级差异。计算公式如下： $$ \text{time_slice}_k= \frac {\text{weight}k}{\sum _ {i=0}^ {n-1}\text{weight} {i}} \cdot \text{sched_latency} $$ 让我们举个例子来看看它是如何工作的。假定有两个工作，A 和 B。A 因为是我们最宝贵的工作，所以优先级较高，nice值为$-5$；B 因为我们不喜欢它，所以优先级为默认值（nice值等于 0）。这意味着$\text{weight}_A$（来自权重表）为 3121，而$\text{weight}_B$ 为 1024。如果计算每个作业的时间片，就会发现 A 的时间片约为sched_latency的 $\frac{3}{4}$（即 $36\text{ms}$），而 B 约为$\frac{1}{4}$（即 $12\text{ms}$）。

除了泛化时间片计算外，CFS计算vruntime的方式也必须进行调整，以下是新公式： $$ \text{vruntime}_i=\text{vruntime}_i+\frac{\text{weight}_0}{\text{weight}_i}\cdot \text{runtime}_i $$ 它根据进程$i$累积的实际运行时间（$\text{runtime}_i$），并与进程的权重成反比。在我们的运行示例中，A 的 vruntime 累积速度是 B 的三分之一。

构建上述权重表的一个巧妙之处在于，当 nice 值的差异恒定时，该表保留了 CPU 比例。例如，如果进程 A 的 nice 值为 5（不是 -5），进程 B 的 nice 值为 10（不是 0），则 CFS 将以与之前完全相同的方式调度它们。

7.3 使用红黑树

如上所述，CFS 的一个重点是效率。对于调度器来说，效率有很多方面，但其中一个方面非常简单：当调度器需要查找下一个要运行的作业时，它应该尽可能快地找到该作业。简单的数据结构（如列表）不具扩展性：现代系统有时由上千个进程组成，因此每隔几毫秒搜索一次长列表会非常浪费。

CFS 通过将进程保留在红黑树上来解决这个问题。红黑树是多种类型的平衡树之一；与简单的二叉树（在最糟糕的插入模式下，它的性能会退化到类似于列表）不同，平衡树需要做一些额外的工作来保持较低的深度，从而确保操作在时间上是$\log$（而非线性）的。

CFS 不会将所有进程都保存在此结构中；相反，只有正在运行（或可运行）的进程才会保存在此结构中。如果某个进程进入休眠状态（例如，等待 I/O 完成或等待网络数据包到达），它就会从进程树中删除，并在其他地方跟踪。

让我们看一个例子来更清楚地说明这一点。假设有十个作业，它们的 vruntime 值分别为：1、5、9、10、14、18、17、21、22 和 24。如果我们将这些作业保存在一个有序列表中，那么查找下一个要运行的作业就很简单了：只需删除第一个元素即可。但是，如果将该作业按顺序放回列表中，我们必须扫描这个列表，寻找正确的位置插入，这是一个 $O(n)$ 运算。任何搜索的效率也很低，平均也需要线性时间。

而在红黑树上保持相同的值可以提高大多数操作的效率，如下图所示。

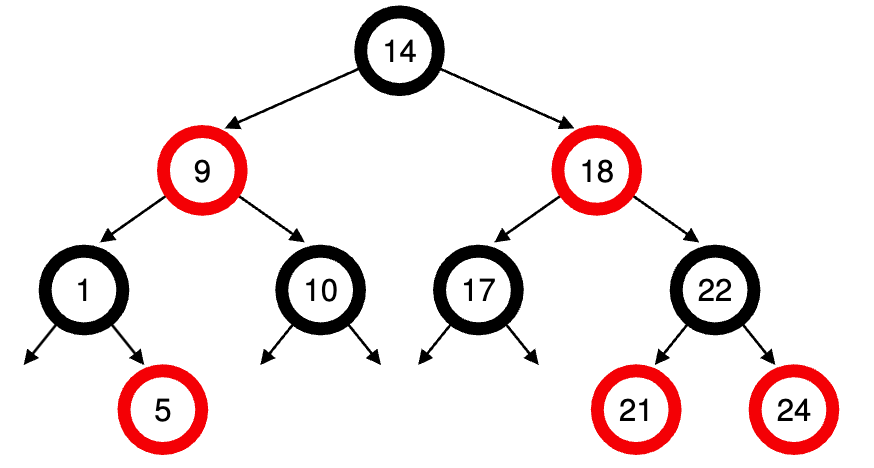
进程在树中按 vruntime 排序，大多数操作（如插入和删除）的时间都是对数级别，即 $O(\log n)$。当 n 越来越大，对数效率明显高于线性效率。

7.4 处理I/O和休眠进程

对于已经进入休眠状态很长一段时间的作业来说，选择下一个运行的最低 vruntime 会出现一个问题。例如有两个进程 A 和 B，其中一个 (A) 连续运行，另一个 (B) 已经进入休眠状态很长一段时间（例如 10 秒）。当 B 醒来时，它的 vruntime 将落后 A 10 秒，因此（如果我们不小心的话），B 现在将在接下来的 10 秒内独占 CPU，同时赶上 A，这实际上会让A饥饿。

CFS 通过在作业唤醒时更改其 vruntime来处理这种情况。具体来说，CFS 会将该作业的 vruntime 设置为在树中找到的最小值（记住，树中只包含正在运行的作业）。通过这种方式，CFS 避免了饥饿，但也并非没有代价：短时间睡眠的作业往往无法获得公平的 CPU 份额。

8 总结

我们介绍了比例份额调度的概念，并简要讨论了三种方法：彩票调度、步幅调度和 Linux 的完全公平调度器（CFS）。彩票调度巧妙地利用随机性来实现比例份额，而步幅调度则是确定性地实现比例份额。CFS 是本章讨论的唯一一种 “真正的 “调度程序，有点像带有动态时间片的加权循环调度程序，但其设计可在负载情况下进行扩展并表现良好；据我们所知，它是目前使用最广泛的公平分配调度程序。

任何调度器都不是万能的，公平共享调度器也有自己的问题。其中一个问题是，这种方法与 I/O 并不十分匹配；如上所述，偶尔执行 I/O 的作业可能无法获得公平分配的 CPU。另一个问题是，它们没有解决彩票或优先级分配的难题，也就是说，你怎么知道应该给你的浏览器分配多少彩票，或者给你的文本编辑器设置nice的值呢？其他通用调度程序（如我们之前讨论过的 MLFQ 和其他类似的 Linux 调度程序）会自动处理这些问题，因此可能更容易部署。

好消息是，在许多领域中，这些问题并不是主要问题，比例份额调度器的使用效果很好。例如，在虚拟化数据中心（或云计算）中，你可能希望将四分之一的 CPU 周期分配给 Windows VM，其余的分配给基本的 Linux 安装，按比例份额可以简单而有效地做到这一点。这个想法还可以扩展到其他地方。