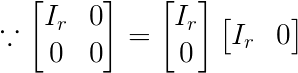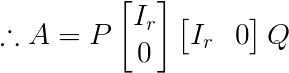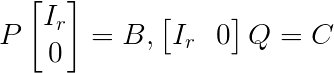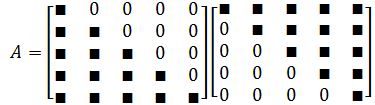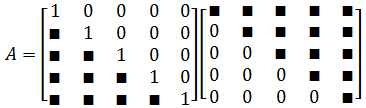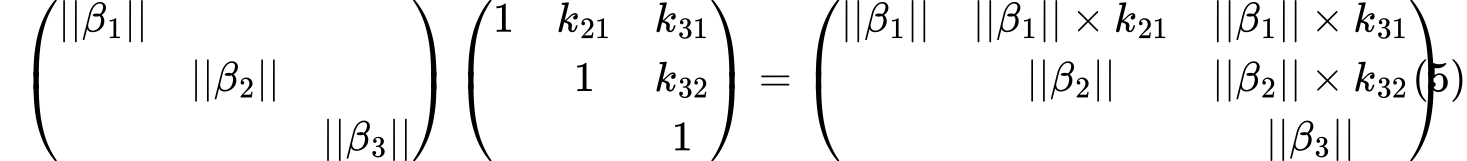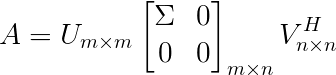HeZephyr贺志飞的博客
HeZephyr贺志飞的博客

【矩阵论】Chapter 6—矩阵分解知识点总结复习（附Python实现）

HeZephyr HeZephyr 收录于 课程笔记 和 矩阵论
  约 4600 字 预计阅读 10 分钟  - 次阅读  

矩阵分解

1 满秩分解（Full-Rank Factorization）

  • 满秩分解定理

    设$m\times n$矩阵$A$的秩为$r>0$，则存在$m\times r$矩阵$B$（列满秩矩阵）和$r\times n$矩阵$C$（行满秩矩阵）使得 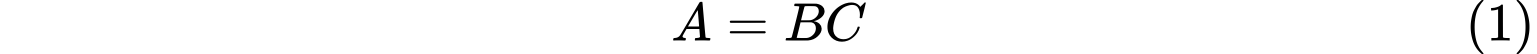image-20240728220206575 并且$rank(B)=rank(C)=r$

    满秩分解不唯一

    定理：设$A$为$m\times n$矩阵，且$rank(A)=r$，存在$m$阶可逆矩阵$P$和$n$阶可逆矩阵$Q$，使得img。

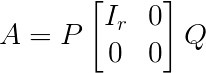    证明满秩分解定理：

    Latex公式渲染之后的图片

    img

    则令img，可得到$A=BC$

    $\because$ $P,C$是可逆矩阵，$B$的$r$个列是$P$的前$r$列；$C$的$r$个行是$Q$的前$r$行

    $\therefore$ $rank(B)=rank(C)=r$

  • 满秩分解步骤

    1. 设$A$为$m\times n$矩阵，首先求$rank(A)$
    2. 取$A$的$j_1,j_2,…j_r$列构成$B_{m\times r}$
    3. 取$A$的Hermite标准型（即行最简行矩阵）$H$的前$r$行构成矩阵$C_{r\times n}$
    4. 则$A=BC$就是矩阵$A$的一个满秩分解

  • Python求解满秩分解

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

    import numpy as np
from sympy import Matrix

'''
Full-Rank Factorization
@params: A Matrix
@return: F, G Matrix
'''
def full_rank(A):
    r = A.rank()
    A_arr1 = np.array(A.tolist())
    # 求解A的最简行阶梯矩阵，要转换成list，再转换成array
    A_rref = np.array(A.rref()[0].tolist())
    k = [] # 存储被选中的列向量的下标
    # 遍历A_rref的行
    for i in range(A_rref.shape[0]):
        # 遍历A_rref的列
        for j in range(A_rref.shape[1]):
            # 遇到1就说明找到了A矩阵的列向量的下标
            # 这些下标的列向量组成F矩阵，然后再找下一行
            if A_rref[i][j] == 1:
                k.append(j)
                break
    # 通过选中的列下标，构建F矩阵       
    B = Matrix(A_arr1[:,k])
    # G就是取行最简行矩阵A的前r行构成的矩阵
    C = Matrix(A_rref[:r])

    return B, C

if __name__ == "__main__":
    # 表示矩阵A
    A = np.array([[1, 1, 0], [0, 1, 1], [-1, 0, 0], [1, 1, 1]])
    A = Matrix(A)
    B, C = full_rank(A)
    print("B:", B)
    print("C:", C)

2 三角分解（Triangular Factorization）

  • $LU$分解定义

    如果有一个矩阵$A$，我们能表示下三角矩阵$L$和上三角矩阵$U$的乘积，称为$A$的三角分解或$LU$分解。

    img

    更进一步，我们希望下三角矩阵的对角元素都为$1$

    img

  • $LU$分解定理

    若$A$是$n$阶非奇异矩阵，则存在唯一的单位下三角矩阵$L$和上三角矩阵$U$使得$A=LU$的充分必要条件是$A$的所有顺序主子式均非零（这一条件保证了对角线元素非零），即$\Delta_k\neq 0(k=1,…,n-1)$

  • $LU$分解步骤

    设$A$为$n\times n$矩阵

    1. 进行初等行变换（注意：不涉及行交换的初等变换），从第$1$行开始，到第$n$行结束。将第$i$行第$i$列以下的元素全部消为$0$
    2. 这样操作后得到的矩阵即为$U$
    3. 构造对角线元素全为$1$的单位下三角矩阵$L$，$L$的剩余元素通过构建方程组的形式来求解。

  • Python求解$LU$分解

  • $LU$分解的实际意义

    • 解线性方程组

      假设我们有一个线性方程组$Ax=b$，其中$A$是一个非奇异矩阵，而$b$是一个列向量。通过$LU$分解，我们可以将方程组转化为两个简化的方程组$Ly=b$和$Ux=y$，其中$L$是下三角矩阵，$U$是上三角矩阵。这两个方程组分别易于求解。

      具体：

      首先，通过前代法（forward substitution）解$Ly=b$，然后通过回代法（backward substitution）解$Ux=y$。这样，我们就得到了方程组的解。

  • $LDU$分解定理

    设$A$是$n$阶非奇异矩阵，则存在唯一的单位下三角矩阵$L$，对角矩阵$D=diag(d_1,d_2,…,d_n)$和上三角矩阵$U$使得$A=LDU$的充分必要条件是$A$的所有顺序主子式均非零（这一条件保证了对角线元素非零），即$\Delta_k\neq 0(k=1,…,n-1)$并且$d_1=a_{11},d_k=\frac{\Delta_k}{\Delta_{k+1}},k=2,…,n$

  • $LDU$分解步骤

    设$A$为$n\times n$矩阵

    1. 先求$LU$分解
    2. 将$U$的对角线元素提出来构成对角矩阵$D$
    3. $U$中的元素$u_{ij}$除以$d_i$，其中$d_i$表示第$i$个对角元素。这样操作得到变换后的$U$

  • Python求解$LDU$分解

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

    import numpy as np
from sympy import Matrix
import pprint

EPSILON = 1e-8

def is_zero(x):
    return abs(x) < EPSILON

def LU(A):
    # 断言A必须是非奇异方阵A
    assert A.rows == A.cols, "Matrix A must be a square matrix"
    assert A.det() != 0, "Matrix A must be a nonsingular matrix"

    n = A.rows

    U = A
    # 构建出U矩阵
    # 将U转换成list，再转换成array
    U = np.array(U.tolist())

    # 遍历U的每一行利用高斯消元法
    for i in range(n):
        # 判断U[i][i]是否为0
        assert not is_zero(U[i][i]), "主元为0，无法进行LU分解"
        # 对i+1行到n行进行消元
        for j in range(i + 1, n):
            # 计算消元因子
            factor = U[j][i] / U[i][i]
            # 对第j行进行消元
            for k in range(i, n):
                U[j][k] -= factor * U[i][k]
    # 消元后的矩阵U则是最终U矩阵
    U = Matrix(U)
    # 根据LU = A，得到L矩阵
    L = A * U.inv()
    return L, U

def LDU(A):
    L, U = LU(A)
    D = Matrix(np.diag(np.diag(U)))
    U = D.inv() * U
    return L, D, U

if __name__ == '__main__':
    A = np.array([[2, 3, 4], [1, 1, 9], [1, 2, -6]])
    A = Matrix(A)
    '''
    # test LU分解
    L, U = LU(A)
    pprint.pprint("L:")
    pprint.pprint(L)
    pprint.pprint("U:")
    pprint.pprint(U)
    '''
    # test LDU分解
    L, D, U = LDU(A)
    pprint.pprint("L:")
    pprint.pprint(L)
    pprint.pprint("D:")
    pprint.pprint(D)
    pprint.pprint("U:")
    pprint.pprint(U)

  • $PLU$分解

    PLU 分解是将矩阵$A$分解成一个置换矩阵$P$、单位下三角矩阵$L$和上三角矩阵$U$的乘积，即 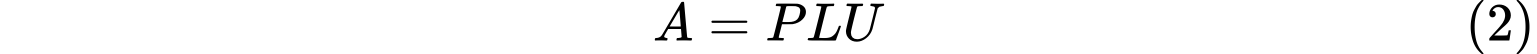image-20240728220231616 之前$LU$分解中限制了行交换，如果不可避免的必须进行行互换，我们就需要进行$PLU$分解。

    实际上只需要把$A = LU$变成$P^{-1}A = P^{-1}PLU$就可以了，实际上所有的$A = LU$都可以写成$P^{-1}A = LU$的形式，由于左乘置换矩阵$P^{-1}$是在交换行的顺序，所以由$P^{-1}A = P^{-1}PLU$推得适当的交换$A$的行的顺序，即可将$A$ 做 $LU$ 分解。当$A$没有行互换时，$P$就是单位矩阵。

    事实上，所有的方阵都可以写成 $PLU$ 分解的形式，事实上，$PLU$ 分解有很高的数值稳定性，因此实用上是很好用的工具。

    有时为了计算上的方便，会同时间换行与列的顺序，此时会将 $A$ 分解成 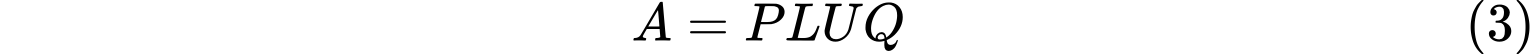image-20240728220240133 其中 $P$、$L$、$U$ 同上，$Q$ 是一个置换矩阵。

3 正交三角分解（QR Factorization）

  • $QR$分解定理

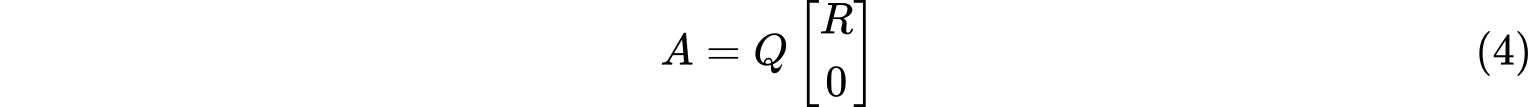
    设$A$是$m\times n$实（复）矩阵，$m\ge n$且其$n$个列向量线性无关，则存在$m$阶正交（酉）矩阵$Q$和$n阶$非奇异实（复）上三角矩阵$R$使得 image-20240728220319602

  • $QR$分解步骤

    设$A$为$3\times 3$矩阵，即$A=(\alpha_1, \alpha_2,\alpha_3)$。则：

    1. 正交化：$\beta_1=\alpha_1$，$\beta_2=\alpha_2-k_{21}\beta_1$，$\beta_3=\alpha_3-k_{31}\beta_1-k_{32}\beta_2$，其中$k_{21}=\frac{<\alpha_2,\beta_1>}{<\beta_1,\beta_1>}$，$k_{31}=\frac{<\alpha_3,\beta_1>}{<\beta_1,\beta_1>}$，$k_{31}=\frac{<\alpha_3,\beta_2>}{<\beta_2,\beta_2>}$。

    2. 单位化得到矩阵$Q$：$Q=(\frac{\beta_1}{||\beta_1||},\frac{\beta_2}{||\beta_2||},\frac{\beta_3}{||\beta_3||})$

    3. 计算得到矩阵$R$： image-20240728220329407

    4. 这样，$A=QR$

  • Python求解$QR$分解

    常规计算：

     1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

    import numpy as np
import sympy
from sympy import Matrix
from sympy import *
import pprint


#正交三角分解（QR）
a = [[1, 1, -1],
     [-1, 1, 1],
     [1, 1, -1],
     [1, 1, 1]]

# a = [[1,1,-1],
#                   [1,0,0],
#                   [0,1,0],
#                   [0,0,1]]
A_mat = Matrix(a)#α向量组成的矩阵A
# A_gs= GramSchmidt(A_mat)
A_arr = np.array(A_mat)
L = []
for i in range(A_mat.shape[1]):
    L.append(A_mat[:,i])
#求Q
A_gs = GramSchmidt(L)#α的施密特正交化得到β
A_gs_norm = GramSchmidt(L,True)#β的单位化得到v

A = []

for i in range(A_mat.shape[1]):
    for j in range(A_mat.shape[0]):
        A.append(A_gs_norm[i][j])#把数排成一行

A_arr = np.array(A)
A_arr = A_arr.reshape((A_mat.shape[0],A_mat.shape[1]),order = 'F')#用reshape重新排列（‘F’为竖着写）
#得到最后的Q
Q = Matrix(A_arr)

#求R

C = []
for i in range(A_mat.shape[1]):
    for j in range(A_mat.shape[1]):
        if i > j:
            C.append(0)
        elif i == j:
            t = np.array(A_gs[i])
            m = np.dot(t.T,t)
            C.append(sympy.sqrt(m[0][0]))
        else:
            t = np.array(A_mat[:,j])
            x = np.array(A_gs_norm[i])
            n = np.dot(t.T,x)
#             print(n)
            C.append(n[0][0])
# C_final为R          
C_arr = np.array(C)
# print(C_arr)
C_arr = C_arr.reshape((A_mat.shape[1],A_mat.shape[1]))
R = Matrix(C_arr)

pprint.pprint("Q:")
pprint.pprint(Q)
pprint.pprint("R:")
pprint.pprint(R)

    调用库函数

    1
2
3
4
5
6
7
8

    # 求矩阵A的QR分解，保留根号
Q_, R_ = A_mat.QRdecomposition()
pprint.pprint("Q_:")
pprint.pprint(Q_)
pprint.pprint("R_:")
pprint.pprint(R_)
assert Q_ == Q, "Q_ != Q"
assert R_ == R, "R_ != R"

4 奇异值分解（SVD）

  • $SVD$定理

    设$A$是$m\times n$矩阵，且$rank(A)=r$，则存在$m$阶酉矩阵$U$和$n$阶酉矩阵$V$使得 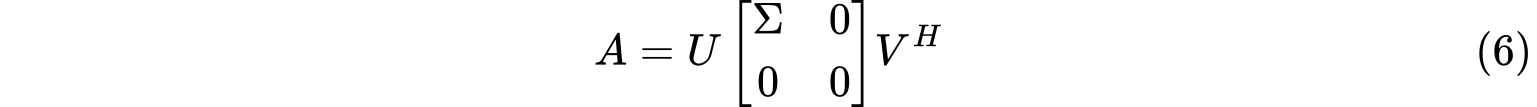image-20240728220417133 其中$\Sigma=diag(\sigma_1,…,\sigma_r)$，且$\sigma_1\geq …\geq \sigma_r>0$。

    $\sigma$为$A$的奇异值，具体含义这里不在叙述，但需要记住的是$\sigma^2$是$A^HA$的特征值，也是$AA^H$的特征值，且：

    1. $A^HA$与$AA^H$的特征值均为非负数
    2. $A^HA$与$AA^H$的非零特征值相同，并且非零特征值的个数（重特征值按重数计算）等于$rank(A)$

    所以我们求$\Sigma$就转换成求这两个矩阵其中一个的特征值。

  • $SVD$分解步骤

    1. 求$A^HA$的$n$个特征值，即计算$|\lambda I-A^HA|=0$。得到特征值：$\lambda_1,…,\lambda_r,\lambda_{r+1}=0,…,\lambda_n=0$，其中$r=rank(A)$。

    2. 将$r$个奇异值（即非零特征值开根号）从大到小排列组成对角矩阵，再添加额外的$0$构成$\Sigma_{m\times n}$矩阵。 image-20240728220426625

    3. 求特征值：$\lambda_1,…,\lambda_r,\lambda_{r+1}=0,…,\lambda_n=0$对应的特征向量$\xi_1,…,\xi_n$：当$\lambda=\lambda_1$时，$(\lambda I-A^HA)\times \xi_1=0$，解得$\xi_1$，同理，计算其余特征向量。

    4. 因为$\xi_1,…,\xi_n$相互正交，我们还需要进行单位化，得到$v_1,…,v_n$，即$v_1=\frac{\xi_1}{||\xi_1||},…,v_n=\frac{\xi_n}{||\xi_n||}$。则$V=(v_1,…,v_n)$。

    5. 根据$A=U_{m\times m}\Sigma_{m\times n}V_{n\times n}^H$，可得$U_1=AV_{n\times n}\Sigma_{r\times n}^{-1}$（注意，$\sigma$此时为$\Sigma_{m\times n}$的前$r$行），易知$U_1$为$m\times r$的矩阵，我们还需要扩充$U_2$，其为$m\times (m-r)$矩阵。

    6. 取$U_1^HU_2=0$，取$U_2$，必须要单位化$U_2$，这样$U=[U_1:U_2]$

    7. 则 img

  • Python求解奇异值分解

     1
 2
 3
 4
 5
 6
 7
 8
 9
10

    import numpy as np
from sympy import Matrix
import pprint

A = np.array([[1,0],[0,1],[1,1]])
# 求A的奇异值分解
U, sigma, VT = np.linalg.svd(A)
print ("U:", U)
print ("sigma:", sigma)
print ("VT:", VT)

相关内容

Buy me a coffee~
HeZephyr 支付宝支付宝
HeZephyr 微信微信
收录于 合集・矩阵论 9
更新于 2024-11-04 
CC BY-NC-SA 4.0
阅读原始文档查看源码编辑此页报告问题
矩阵论
返回 | 主页
0%