【论文阅读笔记】 SkexGen: Autoregressive Generation of CAD Construction Sequences With Disentangled Codebooks

2024-07-19 2024-11-04 约 6800 字预计阅读 14 分钟 - 次阅读

1 摘要

SkexGen是一种新颖的自回归生成模型，用于创建CAD构造序列，其中包含草图和拉伸建模操作。这个模型利用不同的Transformer架构将构造序列中的拓扑、几何和拉伸变化编码到解耦的码本中。自回归Transformer解码器根据码本向量生成具有特定属性的CAD构造序列。广泛的实验表明，我们的解耦码本表示可以生成多样且高质量的CAD模型，增强了用户的控制能力，并能够有效探索设计空间。

【code】

2 引言

SkexGen是一种新颖的自回归生成模型，使用离散码本进行CAD模型生成。作者采用草图和拉伸建模语言来描述CAD构造序列，其中草图操作创建二维原语，拉伸操作将它们提升并组合成三维。Transformer编码器学习到解耦的潜在表示，作为三个码本，分别捕捉构造序列的拓扑、几何和拉伸变化。给定码本向量，自回归Transformer解码器生成草图和拉伸构造序列，进而处理成CAD模型。

作者在一个大规模草图和拉伸数据集（DeepCAD数据集，需要将其转换为SkexGen格式）上评估了SkexGen。与多个baseline和最先进方法进行的定性和定量评估表明，SkexGen生成了更真实和多样的CAD模型，同时实现了有效的控制和高效的设计空间探索，这是以往方法无法实现的。作者做出了以下贡献：

SkexGen架构，自回归生成高质量和多样化的CAD构造序列。
解耦的码本，编码构造序列的拓扑、几何和拉伸变化，实现了设计的有效控制和探索。
在公共基准上的广泛定性和定量评估，展示了最先进的性能。

3 相关工作

构造性实体几何（CSG）
3D形状由参数化基元通过布尔运算组成的CSG树表达。这种轻量级表示已广泛用于与程序合成、神经引导程序合成、无监督学习和专用参数化基元结合的重建任务中。但参数化CAD仍主导机械设计，并且广泛使用草图和拉伸建模操作。
构造序列生成
- PolyGen开创：使用Transformer和指针网络预测n-gon网格顶点和面。
- 数据集推动：大规模CAD建模操作数据集促进直接学习用户建模操作。
- 拉伸操作预测：预测拉伸操作序列以部分恢复构造序列，但没有底层草图信息。预测线、弧、圆等草图基元的序列是形成CAD二维基础的关键构造块，可通过添加拉伸操作轻松扩展到3D。
- Transformer架构的应用：应用于草图和拉伸序列生成，但在用户控制方面存在局限。
现有的方法通常将网络条件设置为用户提供的图像、点云或手绘草图，只是将现有设计转换为CAD构造序列表示，而没有提供对拓扑和几何的单独控制来探索相关设计的空间。作者的方法则提供对拓扑和几何的单独控制。
码本架构
自引入以来，码本已在许多图像和音频生成任务中证明有效，提高了生成图像的多样性并提供了额外的用户控制。由于其高结构规律性，它们特别适合于编码CAD建模序列。

4 草图和拉伸构造序列

作者定义了一个草图和拉伸构造序列表示法，作为基元的层次结构，这一构造基于TurtleGen和DeepCAD的基础，并进行了若干修改，使表示法更具表现力和学习适应性，如下图所示，该示例模型由两个草图组成，这些草图由面、环和曲线构成。序列以拓扑token（$T_1$）开始，表示曲线的起点（类型为弧线），接着两个几何token（$G_1,G_2$），每个token存储一个二维点坐标，。

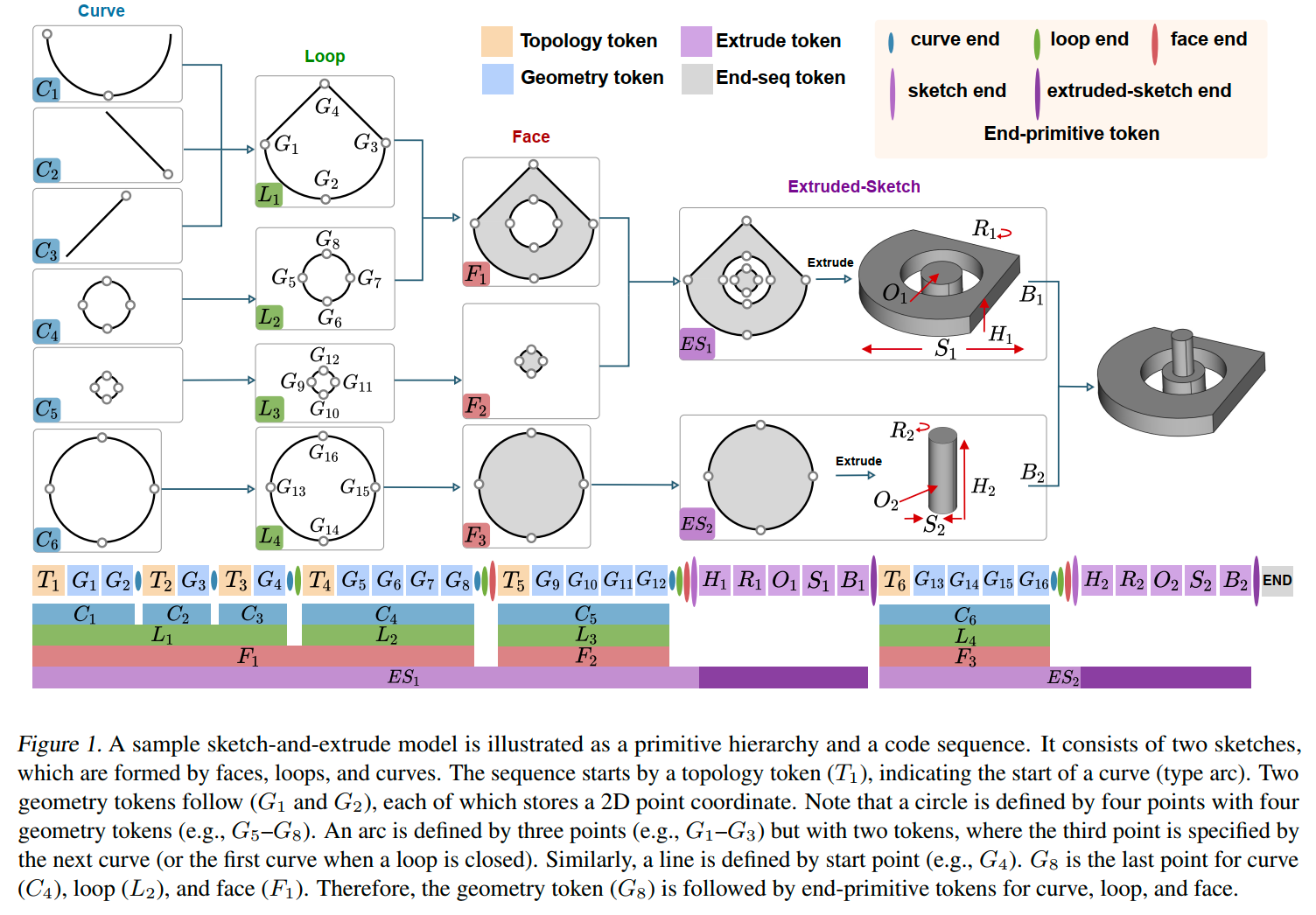
基元层次结构：

曲线：最低级别的基元，包括直线、弧线或圆。
环：一个闭合路径，由一个（例如圆）或多个曲线（例如直线-弧线-直线）组成。
面：一个由环限定的二维区域，这是我们的表示法中新增加的。具体来说，一个面由一个外环和若干内环（洞）构成，这在许多CAD系统中是一个惯例。
草图：由一个或多个面组成。
拉伸草图：通过拉伸草图形成的三维体积。
草图和拉伸模型：通过布尔操作（例如交集、并集和差集）由多个拉伸草图组成。注意，DeepCAD的表示法没有面基元，无法表示具有多个面的草图（例如Figure 1中的ES1）。

5 SkexGen架构

SkexGen 是一种自回归生成模型，通过两个网络分支中的三个解耦码本学习草图和拉伸模型的变体。图2展示了SkexGen的架构。“草图”分支学习二维草图的拓扑和几何变体，“拉伸”分支学习三维拉伸的变体（如方向）。两个分支架构类似，本节重点介绍草图分支，包含两个编码器和一个解码器。

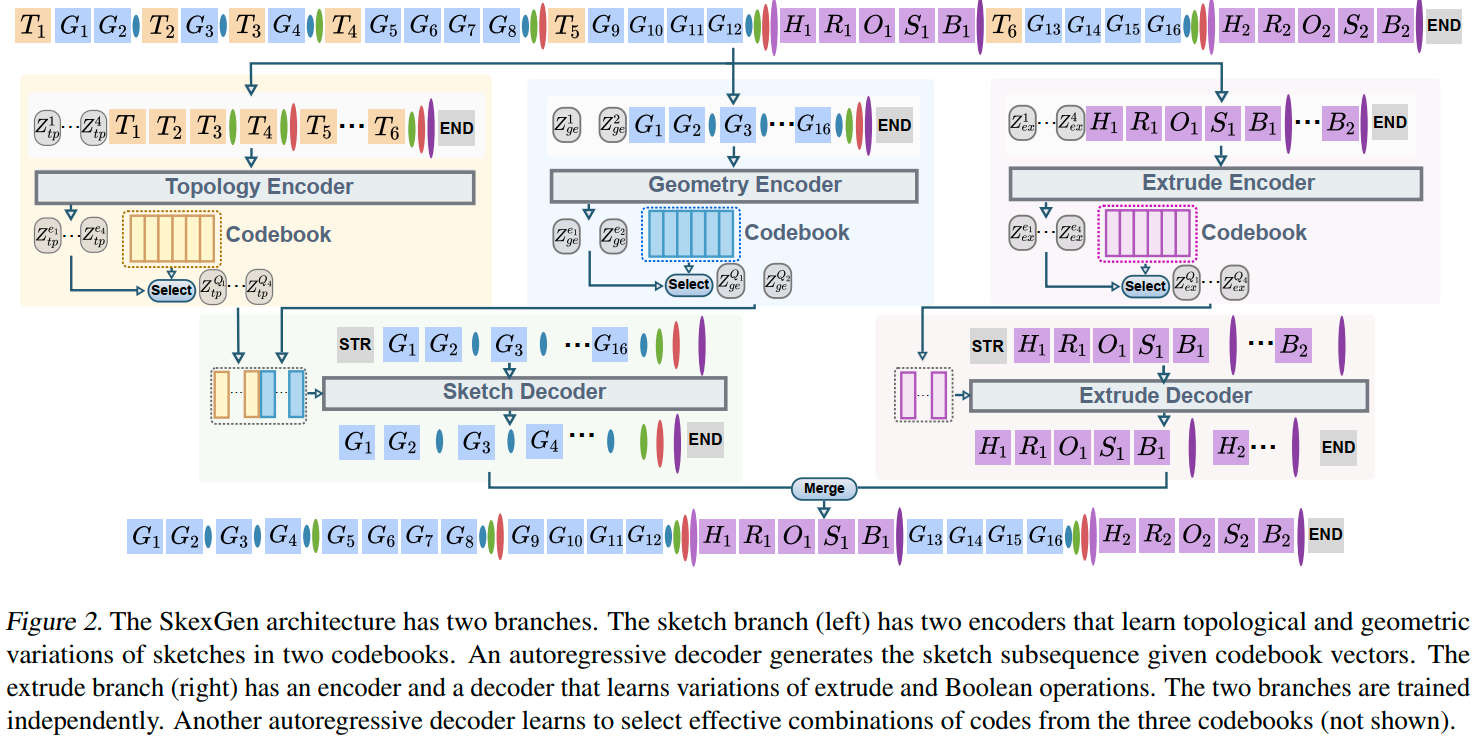
5.1 拓扑编码器

拓扑编码器接收输入的子序列，token为：

拓扑token（T）：表示三种曲线类型之一（直线/弧线/圆）。
结束基元token（E）：表示三种基元类型之一（环/面/草图）的结束。
结束序列token（End）：表示序列的结束。

因此，token初始化为一个7维（= 3+3+1）的独热向量

嵌入
独热向量转换为256维嵌入。作者考虑拓扑token $T$，其中$h_{T} ^{tp}$是7维独热向量，$i_T$表示其在输入子序列中的索引，其嵌入向量计算公式为：
$$ T \leftarrow \mathbf{W}^\text{tp} h_{T} ^{tp} + \mathbf{p}^{(i_T)} $$
其中$\mathbf{W}^\text{tp}\in \mathbb{R}^{d_E\times 7}$表示可学习矩阵，$\mathbf{p}^{(i_T)}$表示拓扑子序列索引$i_T$处的可学习位置编码。
架构
编码器基于Transformer（四层，每层包含八头自注意层、层规范化和前馈层）。根据Vision Transformer，输入的拓扑信息编码为一个“码token”，预先加入到输入中，并初始化为一个可学习的嵌入$Z_{tp}$。令$Z_{tp}^e$为编码器输出的码token嵌入。嵌入$Z_{tp}^e$被量化为大小为$N({\mathbf{b}_{tp}\text{ | }i=1,2\cdots N})$的码本最近码。
编码和量化后的最终码token $Z_{tp}^Q$被传递给解码器。
$$ Z^Q_{tp} \leftarrow \mathbf{b}^{(k)}_{tp}, \text{where } k = \text{argmin}_{j} | Z^e_{_{tp}} - b^{(j)}_{tp} |^2 $$
f这里为了简单起见，只假设了一个码token，拓扑编码器实际上由四个码token，并产生四个输出码token（$Z^{Q_{(1)}}_{tp},Z^{Q_{(2)}}_{tp},Z^{Q_{(3)}}_{tp},Z^{Q_{(4)}}_{tp}$）。作者尝试了不同的码本大小，发现 $N = 500$ 可以取得良好效果。

5.2 几何编码器

输入token
- 几何token（G）：包含一个二维点坐标
- 结束基元token（E）：表示四种基元类型之一（曲线/面/环/草图）的结束
- 结束序列token（End）
几何token G 指定沿曲线的一个二维点坐标。由于坐标是数值型的，作者将草图离散化为$64\times 64$（6位）像素，并考虑$64^2$个可能的像素位置。因此，一个$4101(=64^2+4+1)$维的独热向量唯一确定了token信息。
嵌入
我们按照4.1中的嵌入公式并使用$\mathbf{W^{ge}}\in\mathbb{R}^{d_E\times 4101}$和位置编码来初始化输入token嵌入。token E和End类似于拓扑Token的初始化，通过将它们的独热向量$h^{ge}_G\in \mathbb{R}^{4101}$乘以$\mathbf{W^{ge}}$并加上位置编码。几何Token G的初始化不同：
$$ G \leftarrow \mathbf{W^{ge}} h^{ge}_G + \mathbf{W}^xh^x_G + \mathbf{W}^y h^y_G + \mathbf{p}^{(i_G)}. $$
几何token $G$具有附加的坐标嵌入，$h^x_G,h^y_G\in \mathbb{R}^{64}$是指示像素的$x,y$坐标的独热向量。坐标嵌入是可选的，但可以进一步提高实验结果。
架构
- 类似于拓扑编码器，基于Transformer。
- 生成嵌入 $Z^{{e_{(i)}}}_{ge}$ 和量化后的码token $Z^{Q_{(i)}}_{ge}$ 。
- 使用两个码token，码本大小 $N = 1000$。

5.3 草图解码器

草图解码器以拓扑和几何码本为输入，生成几何token $G$和结束基元token $E$（用于曲线/环/面/草图），以恢复草图子序列。

注意，不生成拓扑标记T，因为它们可以根据每条曲线内的几何标记数量推断出来（即，直线/弧线/圆分别有1/2/4个G标记）。这意味着几何编码器和草图解码器有相似的子序列（Figure 2）。

输入
给定前$k-1$个token，自回归解码器预测第$k$个token的条件概率。训练输入序列向右移一位，前面添加“start”符号（由位置编码初始化）。由于解码器中可能的token类型与几何编码器相同，我们使用相同的$4101$维独热编码方案，并使用带有位置编码的可学习矩阵（大小为 $d_E \times 4101$）初始化嵌入向量。
输出
解码器生成“向左移一位”的子序列，即预测输入中的原始$k$个标记（见Figure 2）。令$K$为草图解码器输出中的一个标记，其具有 $d_E$ 维嵌入。我们使用可学习矩阵 $\mathbf{W^{out}} \in \mathbb{R}^{4101 \times d_E}$ 来预测4101个类别的概率：$h^\text{out}_K \leftarrow \text{softmax} (\mathbf{W^\text{out}} K)$
交叉注意力
Transformer架构通过交叉注意力从拓扑和几何码本中分别取四个和两个量化码本向量。为了区分两个不同的码本，我们借鉴位置编码的思想，分别向拓扑码 ${ Z^{Q_{(i)}}_{tp} }$ 和几何码 ${ Z^{Q_{(i)}}_{ge} }$ 添加可学习嵌入向量 $\mathbf{p}^{(q_{tp})} \in \mathbb{R}^{4 \times d_E}$和 $\mathbf{p}^{(q_{ge})} \in \mathbb{R}^{2 \times d_E}$ ：
$$ Z^{{Q_{(i)}}}_{tp} + p^{(q_{tp})} \quad \text{or} \quad Z^{Q_{(i)}}_{ge}+ p^{(q_{ge})}. $$
基础网络设置与编码器相同（即四层，每层八头），但它是带掩码的自回归（仅关注先前的标记）。

5.4 训练

拓扑编码器、几何编码器和草图解码器通过三种损失函数联合训练：

$$ \sum_K \text{CrossEntropy}(h^\text{out}_K, h^\text{gt}_K) + \ | \text{sg} (Z^{e}_{tp}) - \mathbf{b}_{tp} |_2^2 + \beta | Z^{e}_{tp} - \text{sg} (\mathbf{b}_{tp}) |_2^2 + \ | \text{sg} (Z^{e}_{ge}) - \mathbf{b}_{ge} |_2^2 + \beta | Z^{e}_{ge} - \text{sg} (b_{ge}) |_2^2. $$

第一行计算序列重建损失，其中 $h^\text{out}_K$ 是草图解码器预测的概率， $h^\text{gt}_K$ 是真实的独热向量，利用交叉熵损失衡量准确度。
第二行和第三行是VQ-VAE使用的标准码本和承诺损失。 $\text{sg}$ 表示停止梯度操作，在前向传播中是恒等函数，但在后向传播中阻止梯度。 $\beta$ 缩放承诺损失，设为$0.25$，用于调整承诺损失的权重，这确保编码器输出绑定一个码向量。

为了简化，我们省略了每个编码器中多个码本标记的明确写出。给定一个真实子序列，我们运行两个编码器并自回归地运行解码器，直到生成相同数量的标记。训练采用教师强制的方式，即将真实token而非预测token输入解码器，保证每次迭代解码器仅专注于单步训练，从而简化训练流程并提升效率

5.5 生成

SkexGen 生成 CAD 模型分两步：

从三个码本生成码。
- 采用训练完成的编码器（拓扑、几何、拉伸）从样本中提取码。
- Transformer解码器被训练来生成这些非正态分布的量化码，即从码本中挑选码索引。
- 允许架构微小修改以支持条件码生成，如“拓扑条件码选择器”，它基于给定拓扑码来挑选相应的几何和拉伸码。
给定码生成草图和拉伸构造序列。
- 给定码，草图和拉伸解码器便通过核采样，自回归方式生成构造子序列。
- 这些子序列整合成完整的草图和拉伸序列，最终由CAD软件解析为边界表示。

6 实验

实验验证目标：

SkexGen生成高质量和多样化结果的能力
码本对生成过程控制的程度
SkexGen在设计探索和插值应用中的表现

6.1 实验设置

数据集：使用DeepCAD数据集，包含178,238个序列，经去重和无效操作剔除，最终训练集含74,584个草图子序列与86,417个拉伸子序列。针对单一草图实验，经过从构造序列的步骤中提取草图并去重后，最终收集到114,985个训练样本。
实现细节：SkexGen基于PyTorch开发，在RTX A5000上训练。采用与DeepCAD一致的设置，四层Transformer结构，每层含八个注意力头，层规范化，前馈维度512，输入嵌入256维，Dropout率0.1。使用Adam优化器，学习率0.001。线性预热和梯度裁剪与 DeepCAD 一致。我们在前25个epoch中跳过代码量化，发现这有助于稳定码本训练。对于数据增强，我们向几何标记的坐标添加小的随机噪声。训练300个epoch，批量大小128。草图与拉伸子序列最大长度分别为200与100。在测试时，我们使用核采样方法以自回归方式采样码选择器和解码器。
指标：
- Fréchet Inception Distance (FID)：比较真实和生成数据分布的均值和协方差来衡量生成的保真度。
- 覆盖率（COV）：基于表面上2,000个均匀采样点的最小 Chamfer 距离来衡量真实数据与生成数据的匹配百分比。
- 最小匹配距离 (MMD)：生成样本与其在真实数据集中最近邻的平均最小匹配距离。
- Jensen-Shannon散度 (JSD)：基于边缘点分布衡量真实和生成分布的相似性。
- Novel Score：生成数据中未出现在训练集中的百分比。
- Unique Score：生成样本中仅出现一次的数据百分比，如果序列中的所有token在6位量化后相同，我们认为两个数据样本是相同的。

6.2 随机生成

为了评估 SkexGen 生成高质量和多样化结果的能力，我们随机生成每种类型的20,000个样本，并将 SkexGen 与四个其他基线进行比较：

CurveGen
DeepCAD
单一码本的 SkexGen
带 VAE 的 SkexGen。

由于其他来自同时研究的草图生成模型依赖于草图约束标签，并且理想情况下需要草图约束求解器，这使得它们无法直接比较。

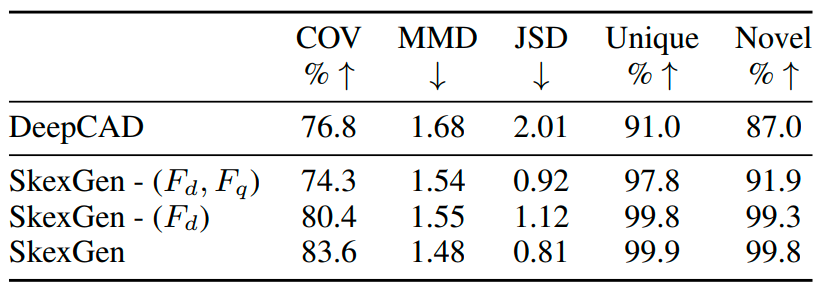
草图生成评估：结果如下表所示。SkexGenFID分数表现最优，证明其生成的草图质量最高。SkexGen在Novel上虽不及DeepCAD，但在Unique上与CurveGen相当或更优。且定性分析显示，DeepCAD虽然Novel得分高，但存在大量无效结果，如自相交曲线和未闭合几何，影响了FID评分。总体而言：

SkexGen 生成的草图在质量上更好，形状更复杂，自相交更少，对称性更强。
CurveGen 也生成了质量不错的结果，但矩形和圆的复杂排列较少。
DeepCAD 可以生成比 CurveGen 更复杂的形状，但噪音很多。

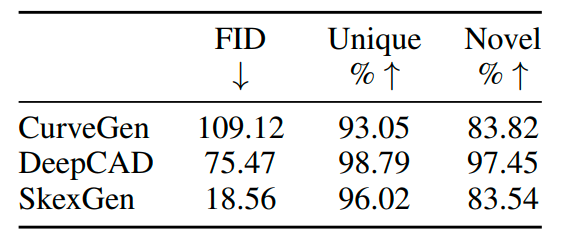
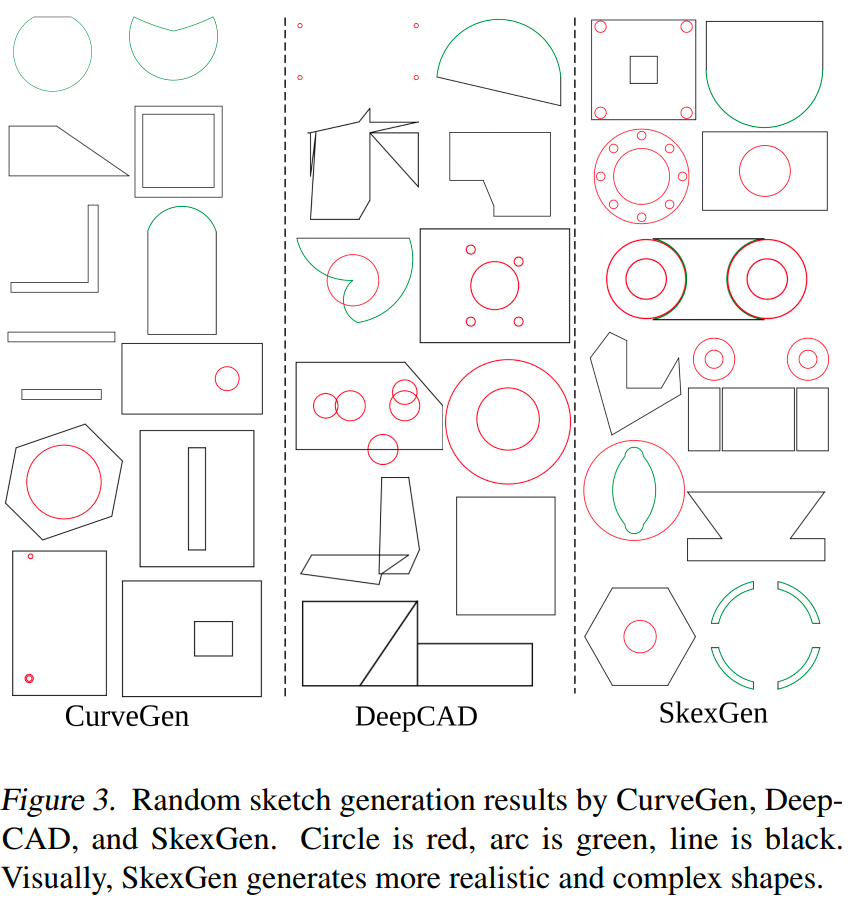
CAD模型生成评估：结果如下表所示，SkexGen在所有评估指标上领先，尤其在形状复杂度、对称性以及频繁使用弧线方面表现出色。SkexGen能生成涉及多步骤草图和拉伸序列的CAD模型，而DeepCAD则主要生成单步模型。表中间两行展示了多个解耦码本的有效性。减少到单个码本后，生成质量下降，SkexGen 类似于 VQ-VAE。当不使用码本时，结果最差，SkexGen 实际上变成了 VAE。

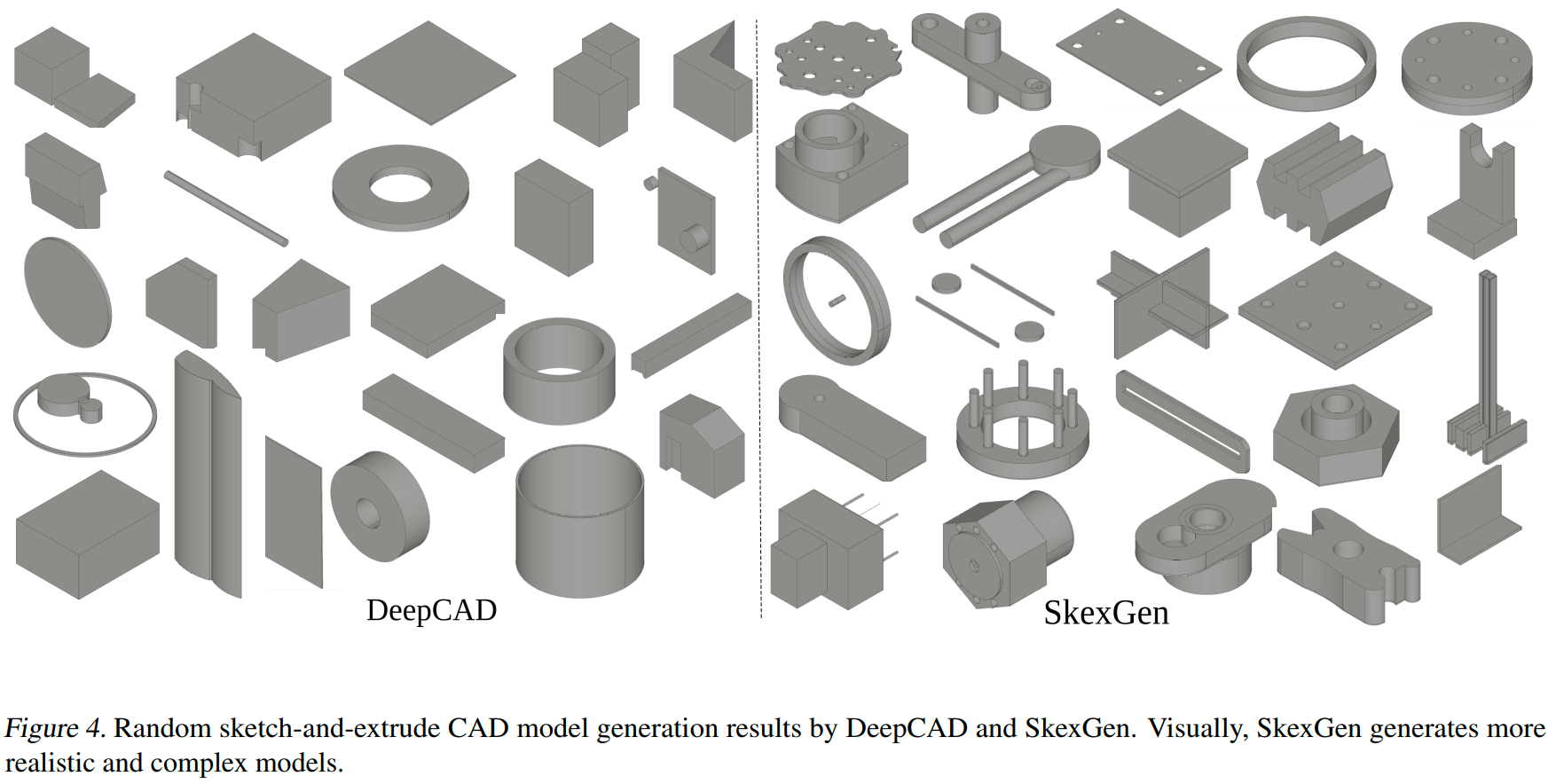
运行时间评估：尽管SkexGen的自回归采样过程使其比DeepCAD慢，但比CurveGen（具有两个依赖的自回归解码器）快，显示出采样效率的优化空间。

6.3 可控生成

解耦码本实现了设计控制与探索，如下图所示：左侧“拓扑条件”：固定拓扑码，其他码通过核采样获得，展示相同结构的不同变体。右侧“几何条件”：固定几何码，改变其他码，体现一致几何下的多样形态。

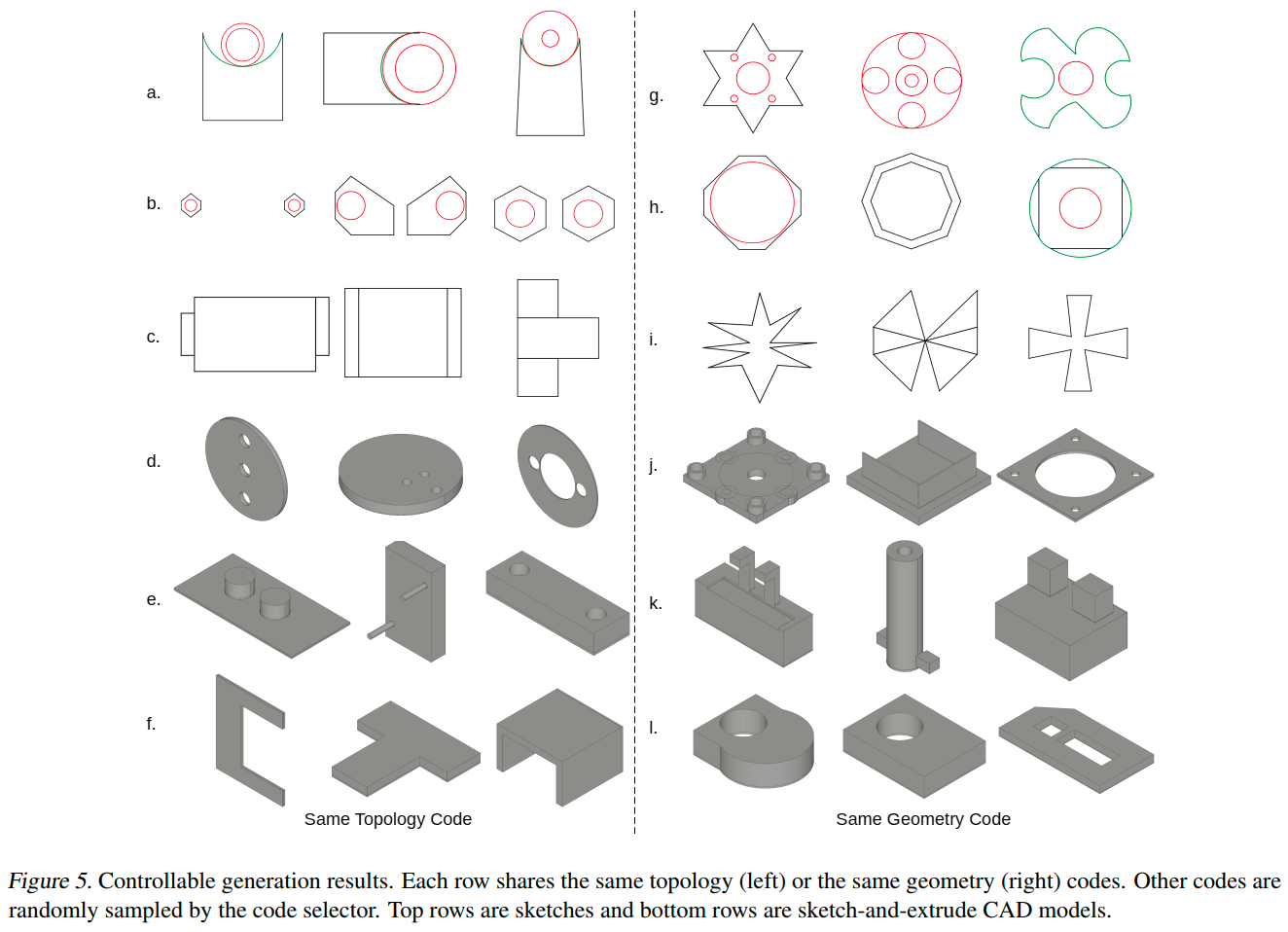
为了定量衡量三个码本之间的解耦程度，作者参考了$\beta\text{-VAE}$的评估方法。通过保持一个拓扑、几何或拉伸标记相同，并对其他部分进行采样，生成一对草图和拉伸序列。然后训练一个小型基于Transformer的分类器，通过编码潜在空间中所有数据对的平均成对差异来识别固定的码。SkexGen的分类准确率为99.8 ± 0.1%，证实码本间解耦效果显著。

6.4 应用

插值应用
利用线性插值技术在模型的码之间探索，生成过渡模型。过程包括：编码模型提取关键码、线性插值这些码，再量化及生成插值模型。插值结果示例如Figure所示，线条演化为圆，矩形实体转为圆形空心盘，显示拓扑和几何动态变化。插值效果可能不平滑，因涉及复杂的离散拓扑变换。
码混合应用
通过混合不同数据的拓扑、几何和拉伸码，创造新颖设计组合。图8示例：保持拓扑形状，调整几何位置，如多个圆柱按方形布局排列。这些混合结果体现了系统的创新设计能力，超越了传统方法的局限。

7 总结

SkexGen是一种新颖的自回归生成模型，专为CAD构造序列设计。它利用不同的Transformer架构将CAD构造序列中的拓扑、几何和拉伸变化编码为解耦码本。这些解码器可以生成具有特定属性的CAD构造序列。SkexGen的优势在于其能够生成多样且高质量的CAD模型，同时提高用户的控制能力和设计空间的探索效率。

模型的评估在一个大规模的CAD数据集上进行，结果表明，SkexGen相比多个基准和最新方法，生成的CAD模型更为真实和多样。此外，SkexGen的架构也增强了用户在设计过程中的控制能力，使其能够更有效地探索不同设计空间。

7.0.1 限制

数据依赖：SkexGen依赖于大量的已标注CAD数据集，这些数据集的质量和多样性直接影响模型的表现。
模型复杂性：该模型使用多个Transformer编码器和解码器来处理复杂的CAD构建序列，这增加了模型的复杂性和计算成本。
拓扑和几何的分离：虽然这种分离有助于提高控制和生成多样性，但在实际应用中可能会导致模型难以学习到拓扑和几何之间的复杂关系。
有限的建模操作：SkexGen主要关注草图和拉伸操作，未涉及其他的CAD建模操作，如旋转、扫掠、布尔运算等，限制了其应用范围（但可以通过导入CAD工具后编辑实现其他CAD建模操作）。

7.0.2 创新点

自回归生成模型：SkexGen是一个自回归生成模型，能够生成高质量和多样化的CAD构建序列。
解耦码本：使用了解耦码本架构，分别编码CAD构建序列中的拓扑、几何和拉伸变化，提高了用户控制和设计空间的探索效率。