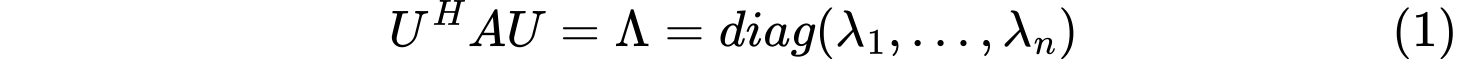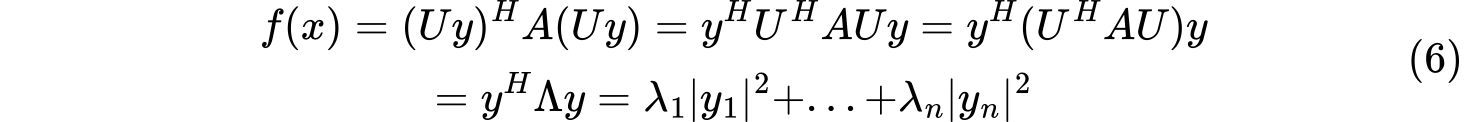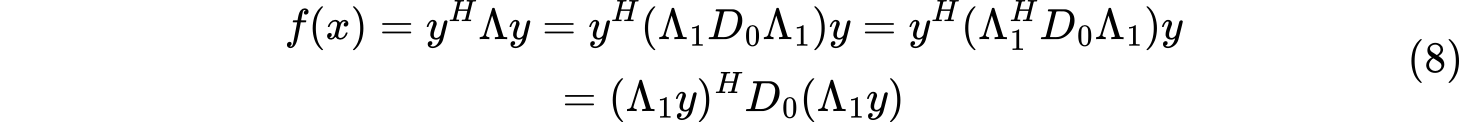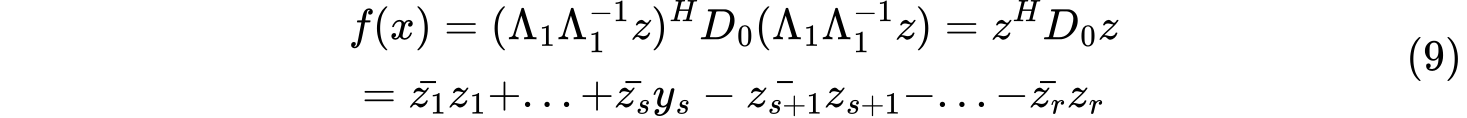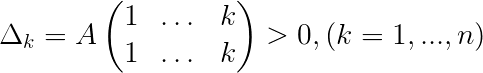【矩阵论】Chapter 7—Hermite矩阵与正定矩阵知识点总结复习

1 Hermite矩阵

• 定义

  设$A$为$n$阶方阵，如果称$A$为Hermite矩阵，则需满足$A^H=A$，其中$A^H$表示$A$的共轭转置，也称Hermite转置，具体操作如下：

  1. 将矩阵的每个元素取共轭。对于复数$a+bi$，它的共轭是$a-bi$，其中$a$和$b$ 是实部和虚部
  2. 将矩阵的行和列互换

  Hermite矩阵与实对称矩阵的性质和证明方法都十分相似

• Hermite矩阵性质

  若$A,B$为$n$阶Hermite矩阵，则

  1. $A$的所有特征值全是实数
  2. $A$的不同特征值所对应的特征向量是相互正交的
  3. 对正整数$k$，$A^k$也是Hermite矩阵
  4. 若$A$可逆，则$A^{-1}$也是Hermite矩阵
  5. 对实数$k,p,kA+pB$也是Hermite矩阵

• Hermite矩阵充分必要条件

  设$A\in C^{n\times n},B\in C^{n\times n}$

  1. $A$是Hermite矩阵的充要条件是存在酉矩阵$U$使得 其中$\lambda_1,…,\lambda_n$均为实数。实对称矩阵则是存在正交矩阵$U…$

  2. A是Hermite矩阵的充要条件是对任意方阵$S$，$S^HAS$是Hermite矩阵

  3. 如果$A,B$是Hermite阵，则$AB$是Hermite矩阵的充要条件是$AB=BA$

• 相合标准形

  设$A$为$n$阶Hermite矩阵，则$A$相合矩阵 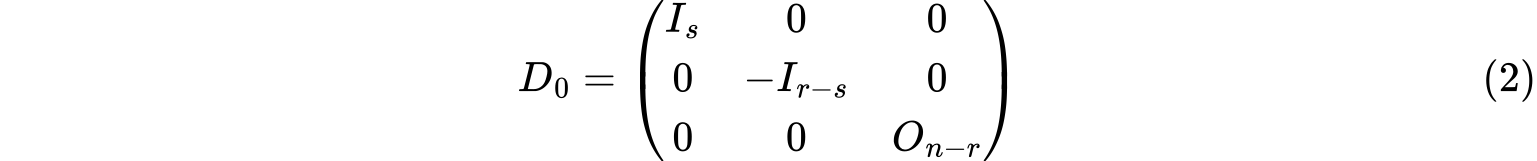其中$r=rank(A)$，$s$是$A$的正特征值（重特征值按重数计算）的个数。矩阵$D_0$则称为$n$阶Hermite矩阵$A$的相合标准形。

• Sylvester惯性定律

  设$A,B$为$n$阶Hermite矩阵，则$A$与$B$相合的充要条件是 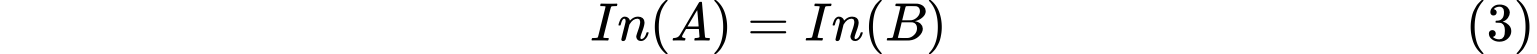其中$In(A)$称为$A$的惯性，$In(A)={\pi(A),v(A),\delta(A)}$。其中$\pi(A)$,$v(A)$,$\delta(A)$分别表示$A$的正、负和零特征值的个数（重特征值按重数计算）。则$A$非奇异的充要条件为$\delta(A)=0$且$\pi(A)+v(A)=rank(A)$。

2 Hermite二次型

• Hermite二次型定义

  由$n$个复变量$x_1,…,x_n$，系数为负数的二次齐式 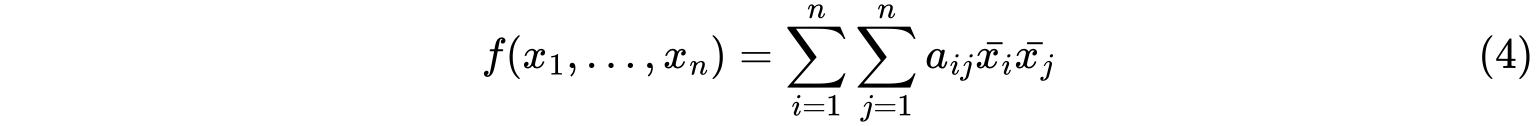其中$a_{ij}=a_{ji}$，称为Hermite二次型。Hermite二次型可写为$f(x)=x^HAx$，我们称$A$的秩就为Hermite二次型的秩。

• Hermite二次型的标准形定理

  对Hermite二次型$f(x)=x^HAx$，存在酉线性变换$x=Uy$（其中$U$是酉矩阵）使得Hermite二次型$f(x)$变成标准形（只包含平方项的二次型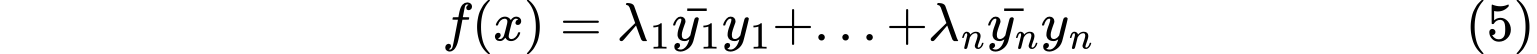） 其中$\lambda_1,…,\lambda_n$为$A$的特征值。

• Hermite二次型化标准形（酉线性变换）

  设$f(x)=x^HAx$，其中$A$为$n$阶Hermite矩阵

  1. 求出二次型矩阵$A$的特征值$\lambda_1,…\lambda_n$和特征向量$v_1,…,v_n$，并将特征向量$v_1,…,v_n$规范正交

  2. 令$U=(v_1,…,v_n),x=Uy$，则

• Hermite二次型规范形定理

  对二次型$f(x)=x^HAx$，存在可逆线性变换$x=Py$使得Hermite二次型$f(x)$化为

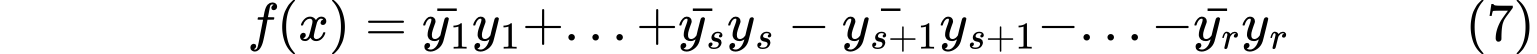
  其中$r=rank(A),s=\pi(A)$。上式则为Hermite二次型$f(x)$的规范形，其中$s$和$(r-s)$分别称为Hermite二次型的正惯性指数和负惯性指数。

• 二次型化规范形

  设$f(x)=x^HAx$，其中$A$为$n$阶Hermite矩阵

  1. 将二次型化为标准形，得到标准形$f(x)=y^H\Lambda y$和酉矩阵$U$

  2. 将对角线元素提取出来，即只保留$\lambda_i$的正负性，则 其中$\Lambda_1$为对角矩阵，对角线元素为$\sqrt {|\lambda_i}|(1\leq i \leq n)$。

  3. 令$y=\Lambda_1^{-1} z$，则

  4. 故$x=U\Lambda^{-1}z$，可逆矩阵$P=U\Lambda^{-1}$

• 正定相关概念

  设$f(x)=x^HAx$为Hermite二次型

  1. 如果$f(x)>0$（等价$s=r=n$），则称$f(x)$为正定的；
  2. 如果$f(x)\geq0$（等价$s=r<n$），则称$f(x)$为半正定（非负定的）的；
  3. 如果$f(x)<0$（等价$s=0,r=n$），则称$f(x)$为负定的；
  4. 如果$f(x)\leq0$（等价$s=0,r<n$），则称$f(x)$为半负定的；
  5. 如果$f(x)$有时为正有时为负（等价$0<s<r\leq n$），则称$f(x)$为不定的；

3 Hermite正定（非负定矩阵）

• 定义

  根据Hermite二次型的正定（非负定）可以定义Hermite矩阵的正定（非负定）。

  设$A$为$n$阶Hermite矩阵，$f(x)=x^HAx$

  1. 如果$f(x)>0$，则称$A$为正定的，记作$A>0$；
  2. 如果$f(x)\geq0$，则称$A$为半正定（非负定的）的，记作$A\geq 0$；
  3. 如果$f(x)<0$，则称$A$为负定的，记作$A<0$；
  4. 如果$f(x)\leq0$，则称$A$为半负定的，记作$A\leq 0$；
  5. 如果$f(x)$有时为正有时为负，则称$A$为不定的；

• 判断$n$阶Hermite矩阵$A$正定

  1. 通过正定矩阵的定义
  2. $A$的$n$个特征值均为正数
  3. $A$的顺序主子式均为正数
  4. $A$的所有主子式全大于$0$
  5. 存在$n$阶非奇异下三角矩阵$L$，使得$A=LL^H$（该分解称为Cholesky分解）
  6. 存在$n$阶非奇异矩阵，使得$A=B^HB$
  7. 存在$n$阶非奇异Hermite矩阵$A=S^2$

• 判断$n$阶Hermite矩阵$A$半正定

  1. 通过半正定矩阵的定义
  2. $A$的$n$个特征值均为非负数
  3. $A$的所有主子式均非负

• 定理证明

  设$A,B$均为$n$阶Hermite矩阵，且$B>0$，则存在非奇异矩阵$P$使得 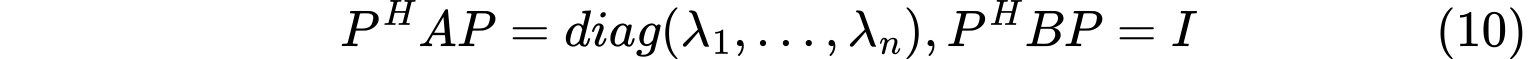其中$\lambda_1,…,\lambda_n$是广义特征值问题的特征值

  证明：

  $\because B >0$

  $\therefore $存在非奇异矩阵$P_1$使得$P_1^HBP_1=I$

  又$\because P_1^HAP_1$仍为Hermite矩阵

  $\therefore$酉矩阵$U$使得 令$P=P_1U$

  $\because P$非奇异，根据定理$P^HBP=I$

  $\therefore P^HBP=(P_1U)^HB(P_1U)=U^HP_1^HBP_1U=I$

  又$\because P_1$非奇异，使得$P_1^HBP_1=I$

  $\therefore$ 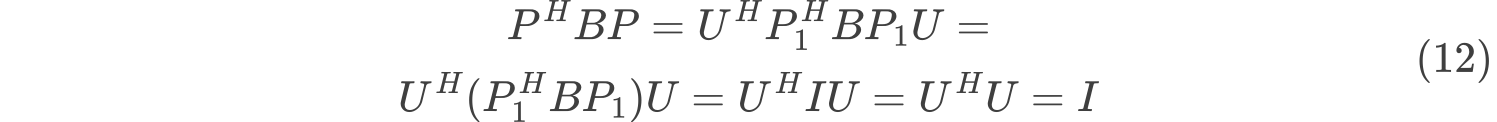$\therefore$ $\therefore$我们可以对$(12)$右乘$P^{-1}$和$B^{-1}$，得到 $\therefore $将$(14)$代入$(13)$中得到 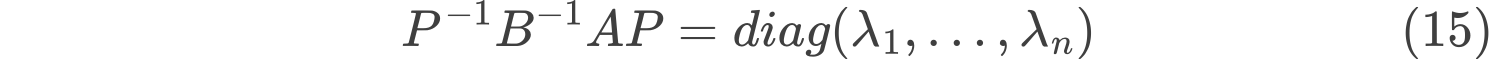即$B^{-1}A$相似于对角矩阵，故$\lambda_1,…,\lambda_n$是矩阵$B^{-1}A$的特征值，即$\lambda_1,…,\lambda_n)$是广义特征值问题的特征值。

  广义特征值问题$Ax=\lambda Bx$，左乘$B^{-1}$，即为$B^{-1}Ax=\lambda x$

4 矩阵不等式

• 定义

  设$A,B$都是$n$阶Hermite矩阵，如果$A-B\geq 0$则称$A$大于或等于$B$（或称$B$小于等于$A$），记作$A\geq B$（或$B\leq A$），即$A-B$半正定；如果$A-B>0$，则称$A$大于$B$（或称$B$小于$A$），记作$A>B$（或$B<A$），即$A-B$正定。

• 性质

  设$A,B,C$均为$n$阶Hermite矩阵，则

  1. $A\geq B(A>B) \Longleftrightarrow-A\leq -B(-A<-B)\Longleftrightarrow$对任意$n$阶可逆矩阵$P$都有$P^HAP\geq P^HBP(P^HAP>P^HBP)$
  2. 若$A>0(A\geq 0),C>0(C\geq 0)$，且$AC=CA$，则$AC>0(AC\geq 0)$
  3. 若$A>B$，$P$为$n\times m$列满秩矩阵，则$P^HAP>P^HBP$
  4. 若$A\geq B$，$P$为$n\times m$矩阵，则$P^HAP\geq P^HBP$

• 定理

  设$A,B$都是$n$阶Hermite矩阵，且$A\geq 0,B>0$，则

  1. $B\geq A$的充要条件是$\rho(AB^{-1})\leq 1$
  2. $B>A$的充要条件是$\rho(AB^{-1})<1$

  设$A$是$n$阶Hermite矩阵，则$\lambda_{min}(A)I\leq A\leq\lambda_{max}I$，这时$\lambda_{min}$和$\lambda_{max}$分别表示$A$的最大和最小特征值。

  设$A,B$均为$n$阶Hermite正定矩阵，则

  1. 若$A\geq B>0$，则$B^{-1}\geq A^{-1}>0$
  2. 若$A>B>0$，则$B^{-1}>A^{-1}>0$

  设$A,B$均为$n$阶Hermite正定矩阵，且$AB=BA$，则

  1. 若$A\geq B$，则$A^2\geq B^2$

     证明：$A^2-B^2=(A-B)(A+B)=(A+B)(A-B)$，易知$(A-B)\geq0,A+B>0$，则克制

  2. 若$A\geq B$，则$A^2> B^2$

     同理得证

  设$A$是$m\times n$行满秩矩阵，$B$是$n\times k$矩阵，则 $$ B^HB\geq (AB)^H(AA^H)^{-1}(AB) $$ 等号成立当且仅当存在一个$m\times k$矩阵$C$使得$B=A^HC$