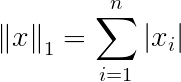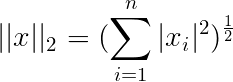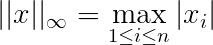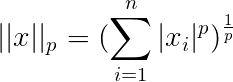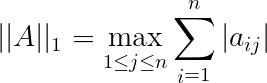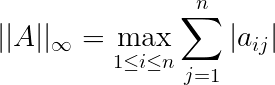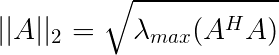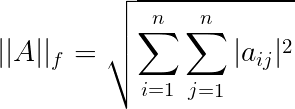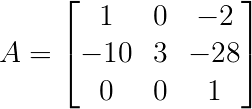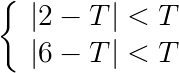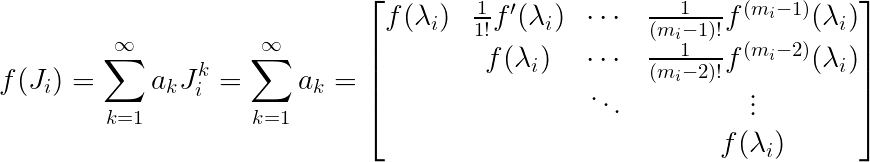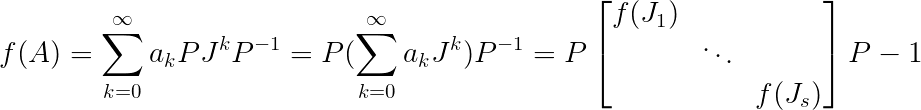【矩阵论】Chapter 8—范数与极限知识点总结复习

2023-12-01 2024-11-04 约 2500 字预计阅读 5 分钟 - 次阅读

1 向量范数

向量范数定义
设$V$是数域$P$上的线性空间，$||x||$是以$V$中的向量$x$为自变量的非负实值函数，如果满足以下三个条件：
1. 非负性：$||x||\geq 0$，且$||x||=0$当且仅当$x=0$
2. 齐次性：$\forall \alpha \in P,x\in V$，有$||\alpha x||=|\alpha|||x||$
3. 三角不等式：$\forall x,y \in V$，有$||x+y||\leq ||x||+||y||$
则称$||x||$为向量$x$的范数，并称定义了范数的线性空间为赋范线性空间。
$1$范数，$2$范数、$\infty$范数和$p$范数
在$n$维向量空间$C^n$中，对任意向量$x=(x_1,…,x_n)^T\in C^n$
$1$范数：
$2$范数：
$\infty$范数：
$p$范数：
利用已知范数构造新范数
设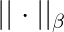是$C^m$上的向量范数，$A\in C^{m\times n}$且$rank(A)=n$，则由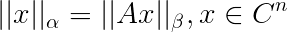所定义的$||\cdot||$是$C^n$上的向量范数
性质
1. 向量范数的等价具有自反性、对称性和传递性
2. 有限维线性空间$V$上的任意两个向量范数都是等价的

2 矩阵范数

矩阵范数定义
设$||A||$是以$C^{m\times n}$中的矩阵$A$为自变量的非负实值函数，如果满足以下四个条件：
1. 非负性：$||A||\geq 0$，且$||A||=0$当且仅当$A=0$
2. 齐次性：$\forall \alpha \in C,A\in C^{m\times n}$，有$||\alpha A||=|\alpha|||A||$
3. 三角不等式：$\forall A,B \in C^{m\times n}$，有$||A+B||\leq ||A||+||B||$
4. 相容性：$\forall A,B \in C^{m\times n}$，有$||AB||\leq ||A||\space ||B||$
则称$||A||$为$m\times n$矩阵$A$的范数
定理
设$A=(a_{ij})\in C^{n\times n}$，则由$l_1,l_2,l_{\infty}$向量范数各自推导得到的矩阵范数
1. 行和范数：
2. 列和范数：
3. 谱范数：
4. $F$范数：

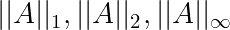
Python求解矩阵范数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
import numpy as np

A = np.matrix([[-1, -1, 4], [1, 1, 2], [1, -2, 2]])

# 表示复数矩阵[[1, -1, 1], [-i, 0, 2i], [1, 1, 1]]
B = np.matrix([[1, -1, 1], [-1j, 0, 2j], [1, 1, 1]])

# 求A的矩阵范数，ord分别为1，2，np.inf，F
print("A范数")
print("A的1范数（列和范数）：", np.linalg.norm(A, ord=1))
print("A的2范数（谱范数）：", np.linalg.norm(A, ord=2))
print("A的无穷范数（行和范数）：", np.linalg.norm(A, ord=np.inf))
print("A的F范数：", np.linalg.norm(A, ord='fro'))

print("B范数")
print("B的1范数（列和范数）：", np.linalg.norm(B, ord=1))
print("B的2范数（谱范数）：", np.linalg.norm(B, ord=2))
print("B的无穷范数（行和范数）：", np.linalg.norm(B, ord=np.inf))
print("B的F范数：", np.linalg.norm(B, ord='fro'))

3 矩阵序列

矩阵序列的收敛
设有矩阵序列${A^{(k)}}$，其中$A^{(k)}=(a_{ij}^{(k)})\in C^{m\times n}$，如果当$k\rightarrow \infty$时，矩阵$A^{(k)}$的每一个元素$a_{ij}^{(k)}$都有极限$a_{ij}$，即 $$ \lim_{k\rightarrow \infty}a_{ij}^{(k)}=a_{ij},1\leq i\leq m;1\leq j\leq n $$ 则称矩阵序列${A^{(k)}}$是收敛的，并把矩阵$A=(a_{ij})\in C^{m\times n}$称为${A^{(k)}}$的极限。
定理
设$A\in C^{n\times n}$，$\lim_{k\rightarrow \infty}A^k=0$的充要条件是$\rho(A)<1$。其中$\rho(A)$为$A$的谱半径，即所有特征值的绝对值的最大值。

4 矩阵级数

矩阵级数定义
设有矩阵序列${A^{(k)}}\in C^{m\times n}$，则无穷和$A^{(1)}+A^{(2)}+…+A^{(k)}+…$称为矩阵级数，记为$\sum_{k=1}^{\infty}A^{(k)}$。由定义可知，矩阵级数收敛的充要条件是$mn$个数项级数$\sum_{k=1}^\infty a_{ij}^{(k)}(1\leq i\leq m, 1\leq j \leq n)$都收敛，如果它们都绝对收敛，则称矩阵级数绝对收敛。
定理
矩阵级数$\sum_{k=1}^{\infty}A^{(k)}$绝对收敛的充要条件是数项级数$\sum_{k=1}^{\infty}||A^{(k)}||$，其中$||\cdot ||$是$C^{m\times n}$上的任一矩阵范数。
矩阵幂级数定义
设$A\in C^{n\times n}$，形如 $$ \sum_{k=0}^{\infty}c_kA^{k}=c_0I+c_1A+c_2A^2+\cdots+c_kA^k+\cdots $$ 的矩阵级数称为矩阵幂级数。
定理
设$A\in C^{n\times n}$，并且幂级数$\sum_{k=0}^{\infty}c_kx^k$的收敛半径为$R$，如果$\rho(A)<R$，则矩阵幂级数$\sum_{k=0}^{\infty}c_kA^k$绝对收敛；如果$\rho(A)>R$，则矩阵幂级数$\sum_{k=0}^{\infty}c_kA^k$发散。
求收敛半径
设幂级数$\sum_{k=0}^{\infty}c_kx^k$
1. 比值法
  $R=\lim_{n\rightarrow \infty}|\frac{a_n}{a_{n+1}}|$
2. 根式法
  $R=\lim_{n\rightarrow \infty}|\frac{1}{\sqrt[n]{a_n}}|$
例题
Given
For $T>0$, find the radius of covergence for $$ s(z)=\sum_{k=0}^{\infty}\frac{1}{(T^3+\frac{3}{k^2+3})^{\frac{k}{3}}}z^k $$ Let $h(z)=s(2z-T)$. Decide when the matrix power series $h(A)$ converges absolutely.
Solution:
For $s(z)$: $R=\lim_{k\rightarrow \infty}\frac{(T^3+\frac{3}{(k+1)^2+3})^{\frac{k+1}{3}}}{(T^3+\frac{3}{k^2+3})^{\frac{k}{3}}}=\lim_{k\rightarrow \infty}\frac{(T^3)^{\frac{k+1}{3}}}{(T^3)^\frac{k}{3}}=T$
So for matrix $2A-TI$, we can determine $|\lambda I-2A+TI|=(\lambda -2+T)^2(\lambda -6 + T)=0$, The eigenvalues are solved as: $2-T,2-T,6-T$.
From , so when $T>3$, $h(A)$ converges absolutly.

5 矩阵函数

矩阵函数定义
设$A\in C^{n\times n}$，一元函数$f(z)$能够展开为$z$的幂级数$f(z)=\sum_{k=0}^\infty c_kz^k$，并且该幂级数的收敛半径为$R$。当矩阵$A$的谱半径$\rho(A)<R$时，则将收敛矩阵幂级数$\sum_{k=0}^{\infty}c_kA^k$的和定义为矩阵函数，记为$f(A)$，即$f(A)=\sum_{k=0}^{\infty}c_kA^k$。
常见矩阵函数
1. 矩阵指数函数：$e^A=\sum_{k=0}^\infty \frac{1}{k!}A^k=I+A+\frac{1}{2!}+\cdots+\frac{1}{n!}A^n+\cdots$
2. 矩阵正弦函数：$sinA=\sum_{k=0}^\infty \frac{(-1)^k}{(2k+1)!}A^{2k+1}=A-\frac{1}{3!}A^3+\frac{1}{5!}A^5-\cdots+(-1)^n\frac{1}{(2n+1)!}A^{2n+1}$
3. 矩阵余弦函数：$cosA=\sum_{k=0}^\infty \frac{(-1)^k}{(2k)!}A^{2k}=A-\frac{1}{2!}A^2+\frac{1}{4!}A^4-\cdots+(-1)^n\frac{1}{(2n)!}A^{2n}$
定理
设$A,B\in C^{n\times n}$，如果$AB=BA$，则$e^Ae^B=e^Be^A=e^{A+B}$。
利用Jordan标准型求矩阵函数$f(A)$
1. 求出矩阵$A$的若当标准型$J$和可逆矩阵$P,P^{-1}$，其中$J=diag(J_1,J_2,\cdots,J_s)$
2. 计算
3. 则

【矩阵论】Chapter 8—范数与极限知识点总结复习

1 向量范数

2 矩阵范数

3 矩阵序列

4 矩阵级数

5 矩阵函数

相关内容