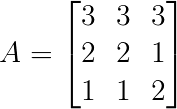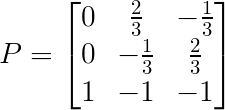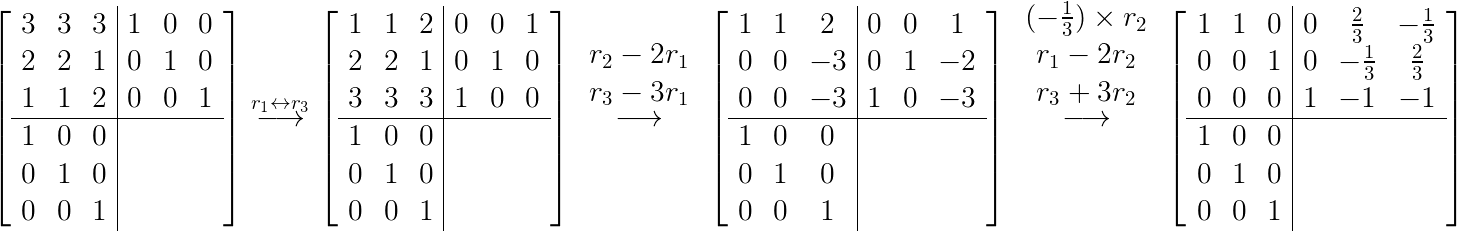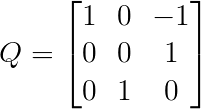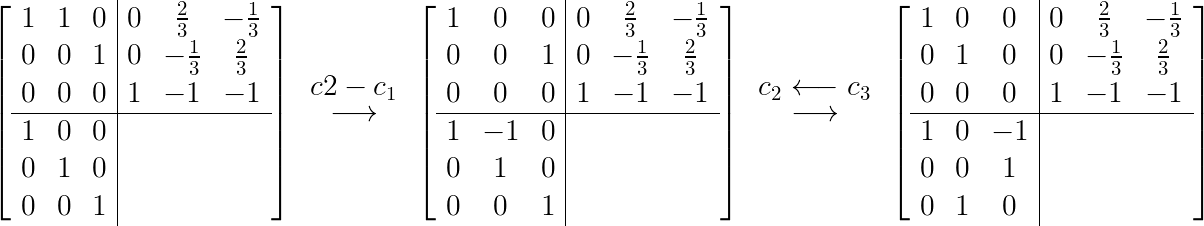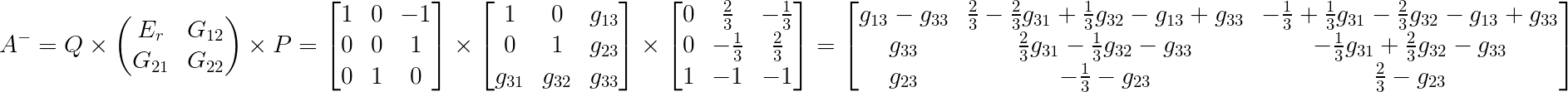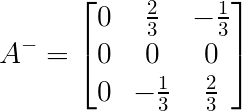【矩阵论】Chapter 9— 广义逆矩阵知识点总结复习

Hermite 标准型实际上就是行最简行

1 广义逆矩阵定义

• 广义逆矩阵$G$ 的定义：对任意$m\times n$ 矩阵的$A$，如果存在某个$n\times m$ 的矩阵$G$，满足 Penrose 方程的一部分或全部，则称$G$ 为$A$ 的广义逆矩阵

  Penrose 方程的四个条件：

  1. $AGA=A$;
  2. $GAG=G$;
  3. $(AG)^T=AG$;
  4. $(GA)^T=GA$

  满足第$i$ 个条件，则把$G$ 记为$A^{(i)}$，这类矩阵的全体记为$A{i}$，所以$A^{i}\in A{i}$

  类似，满足第$i,j$ 个条件：$A^{i,j}\in A{i,j}$

  根据以上，满足$1$ 个，$2$ 个，$3$ 个，$4$ 个 Penrose 方程的广义逆矩阵有$C_4^1+C_4^2+C_4^3+C_4^4=4+6+4+1=15$，但应用最多的，也就是我们所学的以下四种：

  1. 减号逆或者$g$ 逆：$A^-=A^{(1)}$
  2. 最小二乘广义逆：$A_l^-=A^{(1,3)}$
  3. 极小范数广义逆：$A_m^-=A^{(1,4)}$
  4. 加号逆或 Moore-Penrose 广义逆：$A^+=A^{(1,2,3,4)}$

2 减号逆

• $A^-$的性质

  设$A$ 为$m\times n$ 矩阵，$P$ 和$Q$ 分别是$m$ 阶和$n$ 阶非奇异方阵，且$B=PAQ$，$A^-$为 A 的减号逆，则：

  1. $rank(A)\leq rank(A^-)$
  2. $AA^-$和$A^-A$ 是幂等矩阵，并且$rank(AA^-)=rank(A^-A)=rank(A)$
  3. $Q^{-1}A^-P^{-1}\in B{1}$
  4. $A^T{1}={G^T|G\in A{1}}$

• （Penrose 定理）

  设$A,B,C$ 分别为$m\times n,p\times q,m\times q$ 矩阵，则矩阵方程： $$AXB=C$$ 有解的充分必要条件是： $$AA^-CB^-B=C$$ 并且在有解的情况下，其通解为： $$X=A^-CB^-+Y-A^-AYBB^-$$ 其中$Y\in R^{n\times p}$ 是任意的矩阵。

• 求解$A^-$

  $A$ 为$m\times n$ 矩阵 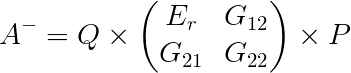，其中$P,Q,E_r$通过对$A$ 进行如下操作得到，$G_{12},G_{21},G_{22}$均为常数矩阵，每一项均用$g_{ij}$表示常数，且$Q,P$ 维度均为$m\times n$，$E_r$是一个$r \times r$ 的对角矩阵，其中$r$ 是矩阵$A$ 的秩，$G_{12}$维度为$m \times (n-r)$ ，$G_{21}$维度为$(m-r) \times n$，$G_{22}$是一个$(m-r) \times (n-r)$ 的矩阵。

  例子

  初等行变换化为行最简阶梯形矩阵，则

  再进行列变换化为$E_r$得到

  则 令$g_{ij}=0$，则

• 利用$A^-$求解线性方程组$Ax=b$

  $Ax=b$ 有解的充分必要条件是$AA^-b=b$，这时特解$x_0=A^-b$，通解$x=A^-b+(I-A^-A)y,\forall y\in C^n$

  这里不给出$A^-$，感兴趣的读者可以自己去实现，具体的算法如下：

  1. 构造水平增广矩阵： 将原矩阵和单位矩阵水平拼接，形成增广矩阵。
  2. 初等行变换： 利用初等行变换将增广矩阵转化为最简行阶梯形式。
  3. 提取$P$：变换后的单位矩阵就是$P$
  4. 构造垂直增广矩阵：再将最简行阶梯形与单位矩阵垂直拼接，形成增广矩阵。
  5. 初等列变换，提取$G$：变换后的单位矩阵就是$G$

3 最小二乘广义逆

• 定理 1

  设$A\in C^{m\times n}$，$G\in A{1,3}$ 的充分必要条件是$G$ 满足 $$A^HAG=A^H$$

  这即为$A{1,3}$（最小二乘广义逆）的通式

• 定理 2

  设$A\in C^{m\times n}$，$A_l^-$是$A$ 的任一最小二乘广义逆，则 $$A{1,3}={G\in C^{n\times m}|AG=AA_l^-}$$

• 定理 3

  设$A$ 是$m\times n$ 矩阵，则$G\in A{1,3}$（即 G 为最小二乘广义逆）的充分必要条件为$x=Gb$ 是不相容线性方程组$Ax=b$ 的最小二乘解。

• 利用$A_l^-$求解线性方程组$Ax=b$

  $x$ 是不相容线性方程组$Ax=b$ 的最小二乘解当且仅当$x$ 是相容线性方程组 $$Ax=AA_l^-b$$ 的解，并且$Ax=b$ 的最小二乘解的通式为$x=A_l^-b+(I-A^-A)y,\forall y\in C^n$

4 极小范数广义逆

• 定理 1

  设$A\in C^{m\times n}$，$G\in A{1,4}$ 的充分必要条件是$G$ 满足 $$GAA^H=A^H$$

  这即为$A{1,4}$（极小范数广义逆）的通式

• 定理 2

  设$A\in C^{m\times n}$，$A_m^-$是$A$ 的任一极小范数广义逆，则 $$A{1,4}={G\in C^{n\times m}|GA=A_m^-A}$$

• 定理$3$

  设$A$ 是$m\times n$ 矩阵，则$G\in A{1,4}$（即 G 为极小范数广义逆）的充分必要条件为$x=Gb$ 是相容线性方程组$Ax=b$ 的极小范数解。

• 利用$A_m^-$求解线性方程组$Ax=b$

  设$A$ 是$m\times n$ 矩阵，则$G\in A{1,4}$ 的充分必要条件为$x=Gb$ 是相容线性方程组$Ax=b$ 的极小范数解，即$x=A_m^-b$ 为相容线性方程组$Ax=b$ 的极小范数解

注意：极小范数解是唯一的，而最小二乘解不唯一

5 Moore-Penrose（加号逆）

• $A^+$ 的性质

  • $A^+$ 存在且唯一
  • $A^+=A_m^-AA_l^-$

• 定理 1

  设$A$ 是$m\times n$ 矩阵，则$G$ 是加号逆$A^+$ 的充分必要条件为$x=Gb$ 是不相容线性方程组$Ax=b$ 的极小最小二乘解。

• 重点

  因为加号逆满足四个条件，所以它也是减号逆、最小二乘广义逆、极小范数广义逆。所以：

  1. 当$b\in R(A)$ 时，$Ax=b$ 的通解为： $$x=A^+b+(I-A^+A)y,\forall y\in R^n$$

  2. 当$b\in R(A)$ 时，$Ax=b$ 的极小范数解为： $$x=A^+b$$ 极小范数解是唯一的

  3. 对于$\forall b$，$Ax=b$ 的最小二乘解为： $$x=A^+b+(I-A^+A)y,\forall y\in R^n$$

  4. 对于$\forall b$，$Ax=b$ 的具有极小范数的最小二乘解为： $$x=A^+b$$

• 求解$A^+$

  1. 若$A$ 为行满秩矩阵，则：$A^+=A^H(AA^H)^{-1}$
  2. 若$A$ 为列满秩矩阵：则：$A^+=(A^HA)^{-1}A^H$
  3. 否则利用满秩分解求解：$A^+=G^+F^+=G^H(GG^H)^{-1}(F^HF)^{-1}F^H$

  Python 代码如下：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  import numpy as np from sympy import Matrix, Symbol def get_A_plus(A): A_plus = None # 判断A是行满秩还是列满秩，如果都不是则利用满秩分解求解A_plus if A.rank() == A.rows: print("A为行满秩矩阵") A_plus = A.H * (A * A.H).inv() elif A.rank() == A.cols: print("A为列满秩矩阵") A_plus = (A.H * A).inv() * A.H else: print("A为非满秩矩阵") # 利用满秩分解求解A_plus，full_rank在另一篇矩阵论复习博客中 F, G = full_rank(A) A_plus = G.H * ((G * G.H).inv()) * ((F.H * F).inv()) * F.H return A_plus

• 利用$A^+$ 求解线性方程组$Ax=b$

  1. $Ax=b$ 有解（相容）的充要条件是$AA^+b=b$
  2. $x=A^+b+(I-A^+A)y,\forall y\in C^n$ 是相容方程组$Ax=b$ 的通解，或是不相容方程组$Ax=b$ 的全部最小二乘解
  3. $x_0=A^+b$ 是相容方程组$Ax=b$ 的唯一极小范数解，或是不相容方程组$Ax=b$ 的唯一极小范数最小二乘解

  Python 代码如下：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

  import numpy as np from sympy import Matrix, Symbol def get_solution(A, b): A_plus = get_A_plus(A) # 单位矩阵 I = Matrix(np.eye(A_plus.rows)) print("I:", I) # 生成符号列表 symbols_list = [Symbol(f'y{i+1}') for i in range(A_plus.rows)] # 生成符号矩阵 symbols_matrix = Matrix(symbols_list) print("symbols_matrix:", symbols_matrix) if A * A_plus * b == b: print("Ax = b有解") print("通解为：") print(A_plus.rows) print(A_plus * b + (I - A_plus * A) * symbols_matrix) print("唯一极小范数解为：") print(A_plus * b) else: print("Ax = b无解") print("全部最小二乘解为：") print(A_plus.rows) print(A_plus * b + (I - A_plus * A) * symbols_matrix) print("唯一极小范数最小二乘解：") print(A_plus * b) get_solution(A, b)