空闲空间管理

1 假设

本讨论的大部分内容将集中于用户级内存分配库中分配器的伟大历史。

我们假设有一个基本接口，例如 malloc() 和 free() 提供的接口。具体来说，void *malloc(size t size) 采用单个参数 size，它是应用程序请求的字节数；它返回一个指向该大小（或更大）的区域的指针（没有特定类型，或者 C 语言中的 void 指针）。补充例程 void free(void *ptr) 接受一个指针并释放相应的块。注意该接口的含义：用户在释放空间时，并不告知库其大小；因此，当只提供指向内存块的指针时，库必须能够计算出内存块有多大。

该库管理的空间历史上称为堆，用于管理堆中空闲空间的通用数据结构是某种空闲列表。该结构包含对托管内存区域中所有空闲空间块的引用。当然，该数据结构本身不必是列表，而只是某种用于跟踪可用空间的数据结构。

我们进一步假设我们主要关注外部碎片。分配器当然也可能存在内部碎片的问题；如果分配器分配的内存块大于请求的内存块，则此类块中任何未请求的（因此未使用的）空间都被视为内部碎片（因为浪费发生在分配的单元内），并且是空间浪费的一种情况。然而，为了简单起见，并且因为它是两种类型的碎片中更有趣的一种，所以我们将主要关注外部碎片。

我们还假设一旦内存被分发给客户端，它就不能被重新定位到内存中的另一个位置。例如，如果程序调用 malloc() 并获得一个指向堆内某个空间的指针，则该内存区域本质上由程序“拥有”（并且不能由库移动），直到程序通过相应的free()调用返回它为止。因此，不可能压缩可用空间，而压缩有助于消除碎片。然而，在实现分段时，可以在操作系统中使用压缩来处理碎片。

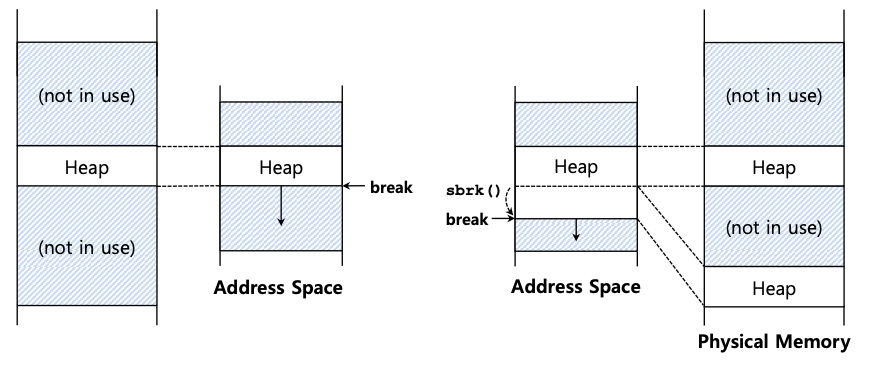
最后，我们假设分配器管理一个连续的字节区域。在某些情况下，分配者可能会要求该区域增长；例如，当空间不足时，用户级内存分配库可能会调用内核来增加堆（通过 sbrk 等系统调用）。然而，为了简单起见，我们假设该区域在其整个生命周期中都是单一的固定大小。

2 低级机制

2.1 分割与合并

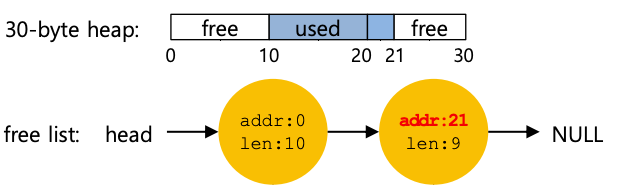
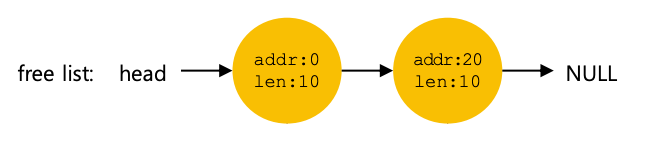
空闲列表包含一组元素，这些元素描述堆中仍剩余的空闲空间。因此，假设有以下 30 字节堆：

该堆的空闲列表上有两个元素。一个条目描述第一个 10 字节空闲段（字节 0-9），一个条目描述另一个空闲段（字节 20-29）：

如上所述，任何大于 10 字节的请求都会失败（返回 NULL），只是没有该大小的连续内存块可用。任何一个空闲块都可以轻松满足对该大小（10 字节）的请求。但如果请求的内容小于 10 个字节，会发生什么情况？

假设我们只请求一个字节的内存。在这种情况下，分配器将执行称为分割的操作：它将找到可以满足请求的空闲内存块并将其分割为两部分。它将返回给调用者的第一个块；第二块将保留在列表中。因此，在上面的示例中，如果发出了 1 个字节的请求，并且分配器决定使用列表中两个元素中的第二个来满足请求，则对 malloc() 的调用将返回 20（分配器的地址）。 1 字节分配区域），列表最终将如下所示：

从图中可以看到列表基本保持完整；唯一的变化是空闲区域现在从 21 而不是 20 开始，并且该空闲区域的长度现在仅为 9。因此，当请求小于任何特定空闲块的大小时，分配器通常会使用分割方法。许多分配器中都有一个推论机制，称为空闲空间合并。再次以上面的例子为例（空闲 10 个字节，已用 10 个字节，还有另外一个空闲 10 个字节）。

给定这个（很小的）堆，当应用程序调用 free(10) 时会发生什么，从而返回堆中间的空间？如果我们只是简单地将这个可用空间添加回我们的列表中而不需要太多思考，我们最终可能会得到一个如下所示的列表：

虽然整个堆现在是空闲的，但它似乎被分为三个块，每个块 10 字节。因此，如果用户请求 20 个字节，简单的列表遍历将找不到这样的空闲块，并返回失败。

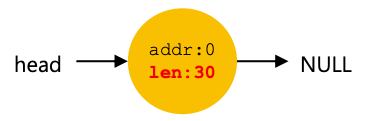
为了避免这个问题，分配器所做的就是在释放一块内存时合并可用空间。这个想法很简单：当返回内存中的空闲块时，仔细查看要返回的块的地址以及附近的空闲空间块；如果新释放的空间紧邻一个（或两个，如本示例中所示）现有空闲块，请将它们合并为一个更大的空闲块。因此，通过合并，我们的最终列表应该如下所示：

事实上，这就是在进行任何分配之前堆列表最初的样子。通过合并，分配器可以更好地确保大的空闲范围可供应用程序使用。

2.2 跟踪分配区域的大小

您可能已经注意到 free(void *ptr) 的接口不采用大小参数；因此，假设给定一个指针，malloc 库可以快速确定正在释放的内存区域的大小，从而将空间合并回空闲列表中。

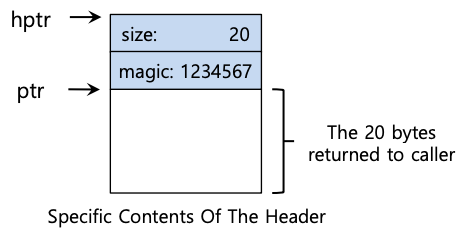
为了完成此任务，大多数分配器在header块中存储一些额外信息，该header块保存在内存中，通常就在分配的内存块之前。让我们再看一个例子，如下图所示。

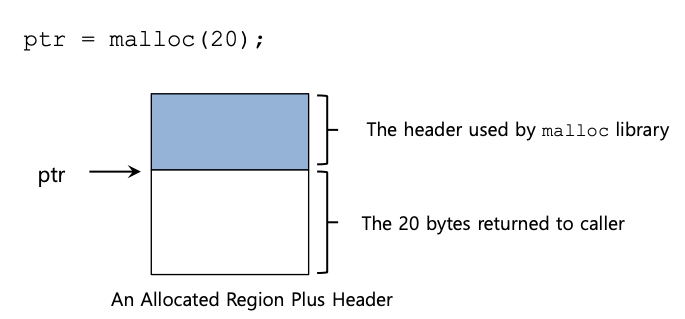
在此示例中，我们正在检查由 ptr 指向的大小为 20 字节的已分配块；想象一下用户调用 malloc() 并将结果存储在 ptr 中，例如 ptr = malloc(20);

header至少包含分配区域的大小（在本例中为 20）；它还可能包含用于加速释放的附加指针、用于提供附加完整性检查的幻数以及其他信息。让我们假设一个简单的标头，其中包含区域的大小和一个幻数，如下所示：

1
2
3
4

typedef struct __header_t {
	int size;
	int magic;
} header_t;

上面的示例如下图所示：

当用户调用 free(ptr)，然后库使用简单的指针算术来确定标头的开始位置：

1
2
3
4

void free(void *ptr) {
	header_t *hptr = (void *)ptr - sizeof(header_t);
    assert(hptr->magic == 1234567 && “Heap is corrupt”);
	...

获得这样一个指向header的指针后，库可以轻松确定幻数是否与预期值匹配作为健全性检查（assert(hptr->magic == 1234567)），并通过简单的数学运算（即，将header的大小添加到区域的大小）计算新释放区域的总大小。请注意最后一句中的小但关键的细节：空闲区域的大小是header的大小加上分配给用户的空间的大小。因此，当用户请求 N 字节的内存时，库不会搜索大小为 N 的空闲块；相反，它会搜索大小为 N 加上header大小的空闲块。

2.3 嵌入空闲列表

到目前为止，我们已经将简单的空闲列表视为一个概念实体；它只是一个描述堆中空闲内存块的列表。但是我们如何在空间空间本身内构建这样的列表呢？

在更典型的列表中，分配新节点时，只需在需要该节点的空间时调用 malloc() 即可。不幸的是，在内存分配库中，你不能这样做！相反，您需要在可用空间本身内构建列表。如果这听起来有点奇怪，请不要担心；是的，但并不奇怪到你做不到！

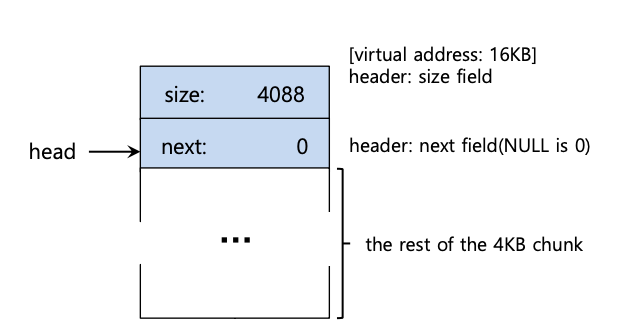
假设我们有一个 4096 字节的内存块需要管理（即堆为 4KB）。要将其作为空闲列表进行管理，我们首先必须初始化该列表；最初，列表应该有一个条目，大小为 4096（减去header大小）。以下是链表节点的描述：

1
2
3
4

typedef struct __node_t {
	int size;
	struct __node_t *next;
} node_t;

现在让我们看一些初始化堆并将空闲列表的第一个元素放入该空间的代码。我们假设堆是在通过调用系统调用 mmap() 获得的一些可用空间内构建的；这不是构建此类堆的唯一方法，但在本例中对我们很有帮助。这是代码：

1
2
3
4
5

// mmap() returns a pointer to a chunk of free space
node_t *head = mmap(NULL, 4096, PROT_READ|PROT_WRITE,
                    MAP_ANON|MAP_PRIVATE, -1, 0);
head->size = 4096 - sizeof(node_t);
head->next = NULL;

运行这段代码后，列表的状态是只有一个条目，大小为 4088。是的，这是一个很小的堆，但它为我们提供了一个很好的例子。

head指针包含该范围的起始地址；我们假设它是 16KB（尽管任何虚拟地址都可以）。从视觉上看，堆看起来就像下面这样。

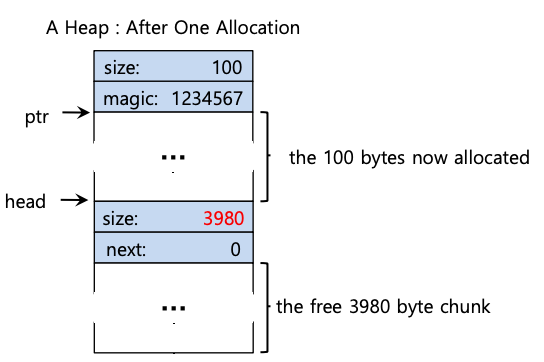
现在，我们假设请求一块内存，大小为 100 字节。为了服务这个请求，库将首先找到一个足够大的块来容纳该请求；因为只有一个空闲块（大小：4088），所以将选择该块。然后，该块将被分割成两部分：一个足够大以服务请求（和header，如上所述），以及剩余的空闲块。假设有一个 8 字节的header（整数大小和整数幻数），堆中的空间现在看起来如下图所示：

因此，在请求 100 字节时，库从现有的一个空闲块中分配了 108 字节，返回一个指向它的指针（上图中标记为 ptr），将header信息存储在分配的空间之前，以便之后供free()使用，并将链表中的一个空闲节点缩小到 3980 字节（4088 减 108）。

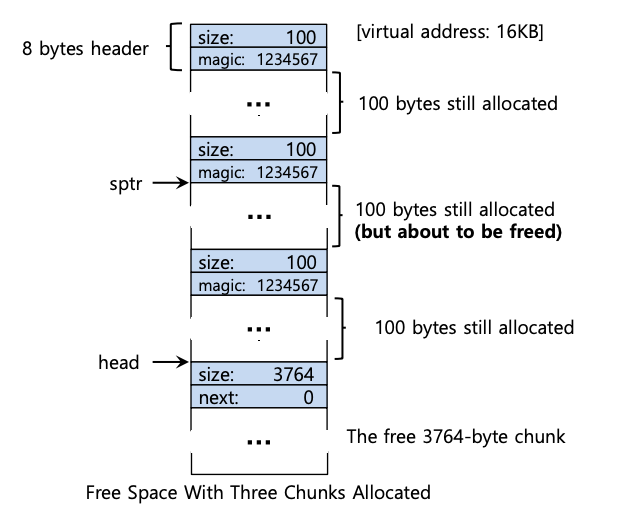
现在让我们看看有 3 个分配区域的堆，每个区域 100 个字节（或 108 个字节，包括header）。该堆的可视化如下图所示。

正如您在其中看到的，堆的前 324 字节现已分配，因此我们在该空间中看到三个header以及调用程序正在使用的三个 100 字节区域。空闲列表仍然无趣：只是一个节点（由head指向），但在三个分割之后现在大小只有 3764 字节。但是当调用程序通过 free() 返回一些内存时会发生什么？

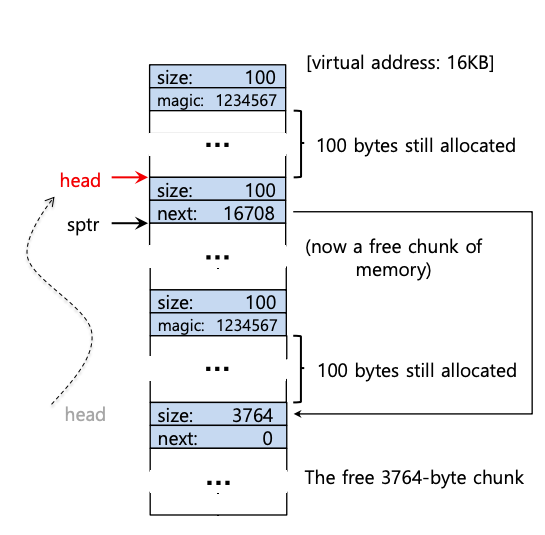
在此示例中，应用程序通过调用 free(16500)（值16500是通过将内存区域的起始地址16384与前一个块的108相加以及此块头部的8字节来得到的。） 返回已分配内存的中间块。该值在上图中由指针 sptr 显示。

库立即计算出空闲区域的大小，然后将空闲块添加回空闲列表。假设我们在空闲列表的头部插入，空间现在看起来如下图所示。

现在，我们有了一个以小空闲块（100 字节，由列表首部指向）和大空闲块（3764 字节）开始的列表。我们的列表终于多了一个元素！是的，空闲空间是支离破碎的，这是一种不幸但常见的现象。

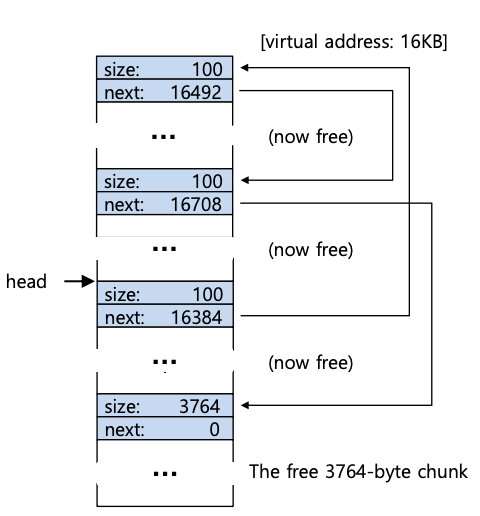
最后一个例子：现在让我们假设最后两个正在使用的块已被释放。如果不进行合并，您最终可能会得到一个高度碎片化的空闲列表，如下图所示。

从图中可以看出，我们现在一团糟！为什么？很简单，我们忘记合并列表。虽然所有的内存都是空闲的，但它却被分割成碎片，因此不是完整的内存，而是呈现出碎片化的内存。解决方案很简单：遍历列表并合并相邻块；完成后，堆将再次完整。

2.4 增加堆

我们应该讨论许多分配库中的最后一种机制。具体来说，如果堆空间不足该怎么办？最简单的方法就是失败。在某些情况下，这是唯一的选择，因此返回 NULL 是一种值得尊敬的方法。

大多数传统分配器都从一个小堆开始，然后在内存耗尽时向操作系统请求更多内存。通常，这意味着它们进行某种系统调用（例如，大多数 UNIX 系统中的 sbrk）来增加堆，然后从那里分配新的块。为了服务 sbrk 请求，操作系统查找空闲物理页，将它们映射到请求进程的地址空间，然后返回新堆末尾的值；此时，可以使用更大的堆，并且可以成功地处理请求，如下图所示。

3 管理空闲空间：基本策略

3.1 最佳适应算法

最佳适应算法的策略非常简单：首先，搜索空闲列表并找到与请求大小一样大或更大的空闲内存块。然后，返回该组候选者中最小的那个；这就是所谓的最佳适应块（也可以称为最小适应）。遍历一次空闲列表就足以找到要返回的正确块。

最佳适应背后的直觉很简单：通过返回接近用户要求的块，最佳适应尝试减少浪费的空间。然而，这是有代价的；当对正确的空闲块执行详尽的搜索时，幼稚的实现会带来严重的性能损失。

3.2 最差适应算法

最差适应算法与最佳适应算法相反；找到最大的块并返回请求的数量；将剩余的（大）块保留在空闲列表中。因此，最差适应尝试留下大块，而不是最佳适应方法可能产生的大量小块。然而，再次需要对可用空间进行全面搜索，因此这种方法的成本可能很高。更糟糕的是，大多数研究表明它的性能很差，导致过多的碎片，同时仍然具有很高的开销。

3.3 首次适应算法

首次适应算法只需找到第一个足够大的区块，并将请求的大小返回给用户。与之前一样，剩余的空闲空间将保留给后续请求。

首次适应算法的优点是速度快，无需穷举搜索所有空闲空间，但有时会用小对象污染空闲列表的开头部分。因此，分配器如何管理空闲列表的顺序就成了一个问题。一种方法是使用基于地址的排序；通过保持列表按空闲空间的地址排序，凝聚变得更容易，碎片也会减少。

3.4 循环首次适应算法

循环首次适应算法并不总是在列表的开头开始首次适应搜索，而是保留一个额外的指针，指向列表中最后一次查找的位置。这个想法是在整个列表中更均匀地分布对可用空间的搜索，从而避免列表开头的分割。这种方法的性能与首次适应算法非常相似，因为再次避免了穷举搜索。

3.5 四种算法实例对比

以下是上述策略的一些示例。设想一个空闲列表，其中包含三个元素，大小分别为 10、30 和 20（这里我们将忽略headers和其他细节，而只关注策略的运作方式）：

假设分配请求大小为 15。最佳适应算法会搜索整个列表并发现 20 是最适合的，因为它是可以容纳请求的最小可用空间。生成的空闲列表：

正如本例中发生的情况，也是最佳适应方法经常发生的情况，现在剩下了一个小的空闲块。最差拟合方法与此类似，但它找到的是最大的块，在本例中为 30。结果列表如下：

在本例中，首次适应算法与最差适应算法执行相同的操作，也是查找可以满足请求的第一个空闲块。区别在于搜索成本；最佳算法和最差算法都会浏览整个列表； 首次适应算法 仅检查空闲块，直到找到适合的块，从而降低搜索成本。

4 其他方法

4.1 隔离列表：slab分配器

一种已经存在一段时间的有趣方法是使用隔离列表。基本思想很简单：如果特定应用程序发出一个（或几个）常见大小的请求，则保留一个单独的列表来管理该大小的对象；所有其他请求都转发到更通用的内存分配器。

这种方法的好处是显而易见的。通过将一块内存专用于特定大小的请求，碎片就不再是一个问题。此外，当分配和释放请求的大小合适时，可以非常快速地处理它们，因为不需要复杂的列表搜索。

但这种方法也会给系统带来新的复杂性。例如，与通用内存池相比，应该将多少内存专门用于服务给定大小的特殊请求的内存池？一个特殊的分配器，由超级工程师 Jeff Bonwick 设计的slab 分配器（设计用于 Solaris 内核），以一种相当好的方式处理这个问题。

具体来说，当内核启动时，它会为可能被频繁请求的内核对象（例如锁、文件系统 inode 等）分配一些对象缓存。因此，对象缓存都是给定大小的隔离空闲列表，并快速服务内存分配和空闲请求。当给定的缓存可用空间不足时，它会从更通用的内存分配器请求一些内存块（slab）（请求的总量是页面大小和相关对象的倍数）。相反，当给定slab内的对象的引用计数全部变为零时，通用分配器可以从专用分配器中回收它们，这通常在VM系统需要更多内存时执行。

通过将列表上的空闲对象保持在预初始化状态，slab 分配器还超越了大多数隔离列表方法。 Bonwick 表明数据结构的初始化和销毁代价高昂 ，通过将特定列表中的已释放对象保持在其初始化状态，slab 分配器因此避免了每个对象的频繁初始化和销毁周期，从而显着降低了开销。

4.2 伙伴分配器

由于合并对于分配器至关重要，因此设计了一些方法来简化合并。二进制伙伴分配器就是一个很好的例子。

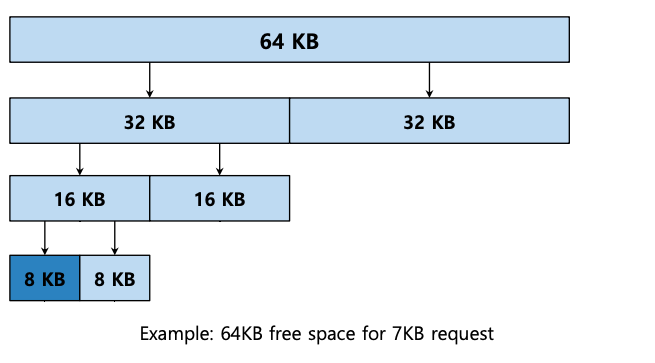
在这样的系统中，空闲内存首先在概念上被认为是大小为 $2^N$ 的大空间。当发出内存请求时，对可用空间的搜索会递归地将可用空间一分为二，直到找到足够大以容纳请求的块（进一步分成两部分将导致空间太小）。此时，所请求的块就返回给用户了。以下是在搜索 7KB 块时划分 64KB 可用空间的示例：

在示例中，最左边的 8KB 块被分配（如较深的蓝色阴影所示）并返回给用户；请注意，该方案可能会受到内部碎片的影响，因为您只能给出两倍大小的块。

伙伴分配的美妙之处在于释放该块时发生的情况。当将8KB块返回到空闲列表时，分配器检查“伙伴”8KB是否空闲；如果是，它将把两个块合并成一个 16KB 的块。然后分配器检查 16KB 块的伙伴是否仍然空闲；如果是这样，它将合并这两个块。这种递归合并过程沿着树继续进行，要么恢复整个可用空间，要么在发现伙伴正在使用时停止。

伙伴分配工作如此顺利的原因是确定特定块的伙伴很简单。想想上面空闲空间中块的地址。如果您仔细思考，您会发现每个好友对的地址仅相差一位；哪一位由好友树中的级别决定。这样您就对二进制好友分配方案的工作原理有了基本的了解。

4.3 其他方法

上述许多方法的一个主要问题是它们缺乏扩展性。具体来说，搜索列表可能会非常慢。因此，高级分配器使用更复杂的数据结构来解决这些成本，以简单性换取性能。例如平衡二叉树、展开树或部分排序树等。

鉴于现代系统通常具有多个处理器并运行多线程工作负载，因此在基于多处理器的系统上花费大量精力使分配器正常工作也就不足为奇了。

Understanding glibc malloc