信号量
1 信号量:定义
信号量是一个具有整数值的对象,我们可以使用两个例程对其进行操作;在 POSIX 标准中,这些例程是 sem_wait() 和 sem_post()。因为信号量的初始值决定了它的行为,所以在调用任何其他例程与信号量交互之前,我们必须首先将其初始化为某个值,代码所下示。
| |
在代码,我们声明了一个信号量 s 并通过将 1 作为第三个参数传递来将其初始化值为 1。在我们将看到的所有示例中,sem_init() 的第二个参数都将设置为 0;**这表明信号量在同一进程中的线程之间共享。**有关信号量其他用法的详细信息(即如何使用它们来同步不同进程之间的访问),请参阅手册页:man sem_init,这需要第二个参数的不同值。
信号量初始化后,我们可以调用两个函数之一与之交互:sem_wait() 或 sem_post()。这两个函数的行为如下所示。
| |
目前,我们不关心这些例程的实施,这显然需要一些小心;当多个线程调用 sem_wait() 和 sem_post() 时,显然需要管理这些临界区。我们现在将重点讨论如何使用这些原语;稍后我们可能会讨论它们是如何构建的。
我们应该在这里讨论接口的几个重要方面。
- 首先,我们可以看到
sem_wait()要么立即返回(因为当我们调用sem_wait()时信号量的值为 1 或更高),要么导致调用者暂停执行以等待后续的操作。当然,多个调用线程可能会调用sem_wait(),因此所有线程都会排队等待被唤醒。 - 其次,我们可以看到
sem_post()不会像sem_wait()那样等待某些特定条件成立。相反,它只是增加信号量的值,然后,如果有一个线程等待被唤醒,则唤醒其中一个线程。 - 第三,信号量的值,当为负时,等于等待线程的数量。虽然信号量的用户一般看不到这个值,但这个不变量还是值得了解的,也许它能帮助你记住信号量的功能。
(暂时)不用担心信号量内可能出现的竞争条件;假设它们所做的操作是原子执行的。我们很快就会使用锁和条件变量来做到这一点。
2 二进制信号量(锁)
我们现在准备使用信号量。我们的第一个用途将是我们已经熟悉的:使用信号量作为锁。代码片段如下;其中,您会看到我们只是用 sem_wait()/sem post() 包围感兴趣的临界区。然而,使这项工作成功的关键是信号量 m 的初始值(代码中初始化为 X)。 X 应该是什么?
| |
回顾上面 sem_wait() 和 sem_post() 例程的定义,我们可以看到初始值应该是 1。
为了清楚起见,让我们想象有两个线程的场景。第一个线程(线程0)调用sem_wait();它首先会递减信号量的值,将其更改为 0。然后,仅当该值不大于或等于 0 时才会等待。因为该值为 0,所以 sem_wait() 将简单地返回,并且调用线程将继续,线程 0 现在可以自由进入临界区。如果当线程 0 在临界区内时没有其他线程尝试获取锁,则当它调用 sem_post() 时,它只会将信号量的值恢复为 1(并且不会唤醒正在等待的线程,因为没有) 。下图显示了该场景的踪迹。
当线程 0 “持有锁”(即,它已调用 sem_wait() 但尚未调用 sem_post()),并且另一个线程(线程 1)尝试通过调用 sem_wait 进入临界区时,会出现更有趣的情况。在这种情况下,线程 1 会将信号量的值递减至 $-1$,从而等待(使其自身进入睡眠状态并放弃处理器)。当线程 0 再次运行时,它最终会调用 sem_post(),将信号量的值递增回零,然后唤醒等待线程(线程 1),线程 1 就能够为自己获取锁。当线程 1 完成时,它将再次增加信号量的值,再次将其恢复为 1。
下图显示了此示例的踪迹。除了线程操作外,图中还显示了每个线程的调度器状态:运行、就绪(即可运行但未运行)和休眠。请特别注意,线程 1 在试图获取已持有的锁时进入了睡眠状态;只有当线程 0 再次运行时,线程 1 才能被唤醒并再次运行。
如果你想通过自己的示例来解决这个问题,可以尝试多个线程排队等待锁的场景。在这种跟踪过程中,semaphore 的值会是多少?
因此,我们可以将 semaphores 用作锁。由于锁只有两种状态(持有和未持有),因此我们有时将用作锁的信号量称为二进制信号量。需要注意的是,如果你只是以这种二进制方式使用一个信号量,那么它的实现方式可能比我们在这里介绍的通用信号量更简单。
3 用于排序的信号量
信号量对于对并发程序中的事件进行排序也很有用。例如,线程可能希望等待列表变为非空,以便可以从中删除元素。在这种使用模式中,我们经常发现一个线程等待某件事发生,而另一个线程使某件事发生,然后发出信号表明它已经发生,从而唤醒等待的线程。因此,我们使用信号量作为排序原语(类似于我们之前使用条件变量)。
下面是一个简单的例子。设想一个线程创建了另一个线程,然后想等待它完成执行。
| |
当这个程序运行时,我们希望看到以下内容:
| |
那么问题来了,如何使用信号量来达到这样的效果?事实证明,答案相对容易理解。正如您在代码中看到的,父线程只需调用 sem_wait() ,则子线程 调用sem_post() ,等待子线程完成执行的条件变为 true。然而,这就提出了一个问题:这个信号量的初始值应该是多少?
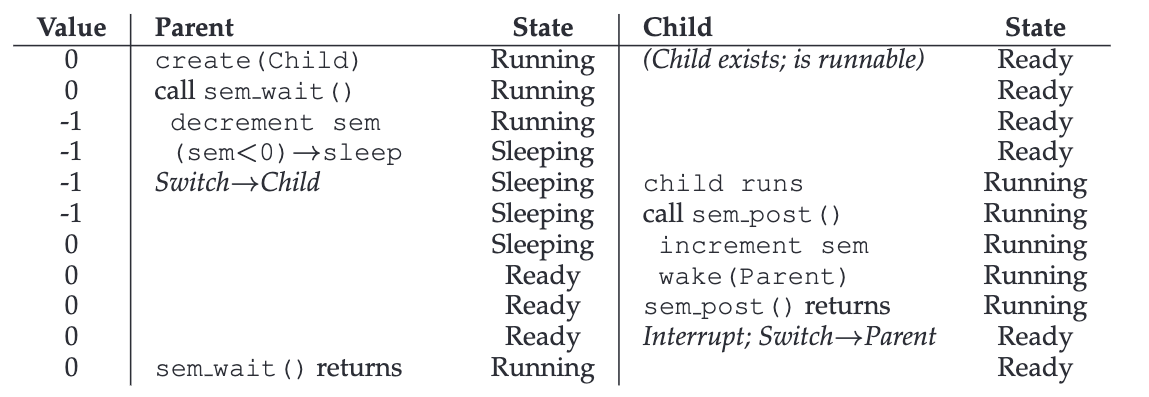
答案当然是信号量的值应该设置为0。有两种情况需要考虑。首先,我们假设父线程创建了子线程,但子线程尚未运行(即,它位于就绪队列中但未运行)。在这种情况下,如下图所示,父线程将子线程调用 sem_post() 之前调用 sem_wait();我们希望父线程等待子线程运行起来。
发生这种情况的唯一方法是信号量的值不大于 0;因此,0 是初始值。父进程运行,将信号量递减(至 -1),然后等待(睡眠)。当子进程最终运行时,它将调用 sem_post(),将信号量的值增加到 0,并唤醒父进程,然后父进程将从 sem_wait() 返回并完成程序。
第二种情况发生在子线程在父线程有机会调用sem_wait() 之前运行完成时,运行跟踪如下图所示。在这种情况下,子线程将首先调用 sem_post(),从而将信号量的值从 0 增加到 1。当父线程有机会运行时,它将调用 sem_wait() 并发现信号量的值为 1;因此,父线程将递减该值(到 0)并从 sem_wait() 返回,无需等待,也达到了预期的效果。
4 生产者/消费者(有界缓冲区)问题
4.1 首次尝试
我们解决这个问题的首次尝试引入了两个信号量:empty 和 full,线程将分别使用它们来指示缓冲区条目何时被清空或填满。下面是解决生产者和消费者问题的首次尝试代码。
| |
在这个示例中,生产者首先等待缓冲区变空,然后将数据放入缓冲区,而消费者同样等待缓冲区被填满,然后才使用缓冲区。让我们先假设 MAX=1(数组中只有一个缓冲区),看看这样是否可行。
再假设有两个线程,一个生产者,一个消费者。让我们看看在单 CPU 上的具体情况。假设消费者先运行。因此,消费者将运行代码中的 C1 行,调用 sem_wait(&full)。由于 full 的初始化值为 0,因此调用将递减 full(至 -1),阻塞消费者,并等待另一个线程按预期在 full 上调用 sem_post()。
假设生产者随后运行。它将运行到 P1 行,从而调用 sem_wait(&empty) 例程。与消费者不同,生产者将继续运行这一行,因为 empty 已被初始化为 MAX 值(在本例中为 1)。因此,empty 将被递减为 0,生产者将把一个数据值放入缓冲区的第一个入口(P2 行)。然后,生产者将继续运行到 P3 行,并调用 sem_post(&full),将 full 信号量的值从 -1 改为 0,并唤醒消费者(例如,将其从阻塞状态转为就绪状态)。
在这种情况下,可能会发生两种情况。如果生产者继续运行,它将循环并再次运行 P1 行。如果生产者被中断,消费者开始运行,它将调用 sem_wait(&full)(C1 行),发现缓冲区确实已满,从而消耗掉缓冲区。无论哪种情况,我们都实现了所需的行为。
你可以用更多线程(例如多个生产者和多个消费者)来尝试这个例子。它应该仍然有效。
现在让我们假设 MAX 大于 1(比如 MAX = 10)。在这个例子中,我们假设有多个生产者和多个消费者。现在我们遇到了一个问题:竞争条件。仔细看看 put() 和get() 代码。想象一下,两个生产者($P_a$ 和 $P_b$)同时调用 put()。假设生产者 $P_a$ 首先运行,并开始填充第一个缓冲区条目(F1 行的 fill = 0)。$P_a$ 还没来得及将fill计数器递增到 1,就被中断了。生产者 $P_b$ 开始运行,并在第 F1 行将其数据放入缓冲区的第 0 个元素,这意味着那里的旧数据被覆盖!这是不允许的;我们不希望生产者的任何数据丢失。
4.2 一个解决方案:添加互斥
正如你所看到的,我们在这里忘记了互斥。缓冲区的填充和缓冲区索引的递增是一个临界区,因此必须小心保护。因此,让我们使用我们的二进制信号量并添加一些锁,代码如下。
| |
4.3 避免死锁
现在,我们在代码的整个 put()/get() 部分添加了一些锁,如 NEW LINE 注释所示。这似乎是个正确的想法,但却行不通。为什么?死锁。为什么会出现死锁?想象一下两个线程,一个生产者,一个消费者。消费者先运行。它获取了mutex(C0 行),然后在full信号量上调用 sem_wait()(C1 行);由于还没有数据,这个调用会导致消费者阻塞,从而占用 CPU;但重要的是,消费者仍然持有锁。
然后生产者运行。如果它能运行,就能唤醒消费者线程,一切都会好起来。不幸的是,它做的第一件事就是调用二进制 mutex信号量(P0 行)上的 sem_wait()。该锁已被锁定。因此,生产者现在也只能等待。
这里有一个简单的循环。消费者持有mutex,正在等待某人发出full的信号。生产者可以发出full的信号,但也在等待mutex。因此,生产者和消费者都在互相等待:这就是典型的死锁。
4.4 可行的解决方案
要解决这个问题,我们只需缩小锁的范围。下面代码显示了正确的解决方案。
| |
正如你所看到的,我们只需将mutex获取和释放移到临界区附近;而full等待empty空等待以及信号代码则留在外部。这就是一个简单而有效的有界缓冲区,是多线程程序中常用的模式。
5 读者—写者锁
另一个经典问题源于人们对更灵活的锁定原语的渴望,即不同的数据结构访问可能需要不同类型的锁定。举例来说,假设有许多并发的列表操作,包括插入和简单的查找。插入操作会改变 list 的状态(因此传统的临界区是合理的),而查找操作只是读取数据结构;只要我们能保证没有插入操作正在进行,我们就能允许许多查找操作并发进行。我们现在要开发的支持这种操作的特殊类型锁被称为读写锁。这种锁的代码如下所示:
| |
代码非常简单。如果某个线程想要更新相关数据结构,它应该调用一对新的同步操作:rwlock_acquire_writelock()(获取写锁)和 rwlock_release_ writelock()(释放写锁)。在内部,这些操作只是使用writelock信号量来确保只有单个写者可以获取锁,从而进入临界区更新相关数据结构。
更有趣的是一对获取和释放读锁的例程。在获取读取锁时,读者首先获取锁,然后递增 readers 变量,以跟踪当前数据结构中有多少个读者。当第一个读者获得锁时,rwlock_acquire_readlock() 中的重要步骤就开始了;在这种情况下,读者也会通过调用writelock信号量上的 sem_wait() 来获得写锁,然后通过调用 sem_post() 来释放锁。
因此,一旦一个读者获得了读锁,就会允许更多读者也获得读锁;但是,任何希望获得写锁的线程都必须等到所有读者都读完;最后一个退出临界区的线程会调用 writelock 信号量上的sem_post(),从而让等待的写者获得写锁。
这种方法有效(如预期),但也有一些负面影响,特别是在公平性方面。特别是,读者饿死写者是相对容易的。对于这个问题存在更复杂的解决方案;也许你能想到更好的实现?提示:考虑一下一旦写者正在等待,您需要做什么来防止更多的读取者进入锁。
读者饿死写者的问题可以通过修改读者和写者的优先级策略来解决。具体思路如下:
- 增加写者优先策略:让写者优先于读者获取锁,这样当有写者等待时,新到来的读者需要等待写者完成后才能进入临界区。
- 写者优先锁设计:引入一个额外的变量或信号量来表示写者是否在等待,如果有写者等待,读者需要等待写者完成后才能获取锁。
最后,应该注意的是,应该谨慎使用读写锁。它们通常会增加更多的开销(特别是对于更复杂的实现),因此与仅使用简单且快速的锁定原语相比,最终不会提高性能。不管怎样,它们再次展示了我们如何以有趣且有用的方式使用信号量。
TIP:简单而愚蠢的方法可能更好(希尔定律) 你永远不应该低估这样一种观念:简单而愚蠢的方法可能是最好的方法。对于锁定,有时简单的自旋锁效果最好,因为它易于实现且速度快。虽然读/写锁之类的东西听起来很酷,但它们很复杂,而复杂可能意味着缓慢。因此,总是先尝试简单而愚蠢的方法。这种追求简单的想法在很多地方都可以找到。早期的一个来源是 Mark Hill 的论文,该论文研究了如何为 CPU 设计缓存。 Hill 发现简单的直接映射缓存比花哨的集合关联设计效果更好(原因之一是在缓存中,更简单的设计可以实现更快的查找)。正如希尔简洁地总结他的工作:“大而笨更好。”因此,我们将类似的建议称为希尔定律。
6 哲学家就餐问题
6.1 基本介绍
Dijkstra 提出并解决的一个最著名的并发问题被称为 “哲学家就餐问题”。这个问题之所以有名,是因为它很有趣,在智力上也有点意思;然而,它的实际效用却很低。
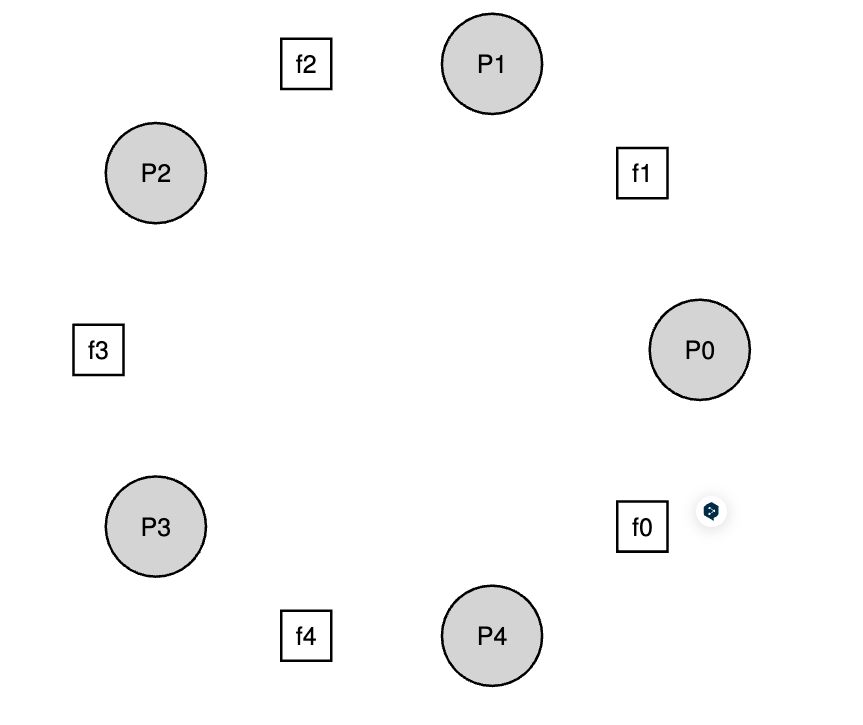
问题的基本设置是这样的,如下图所示:假设有五位 “哲学家 “围坐在一张桌子旁。每对 “哲学家 “之间有一把叉子(因此一共有五把叉子)。哲学家们有思考的时候,不需要叉子,也有吃饭的时候。为了吃饭,哲学家需要两把叉子,左边的和右边的。对这些叉子的争夺以及随之而来的同步问题,正是我们在并发编程中要研究的问题。
这是每个哲学家的基本循环:
| |
那么,关键的挑战是编写例程 getforks() 和 putforks(),这样就不会出现死锁,不会有哲学家挨饿而永远吃不到东西,并且并发性很高(即,许多哲学家可以同时吃饭)尽可能)。
我们将使用一些辅助函数来找到解决方案,如下:
| |
当哲学家 $p$ 希望引用他们左边的叉子时,他们只需调用 left(p)。类似地,通过调用 right(p) 来引用哲学家 $p$ 右边的叉子;其中的模运算符处理最后一个哲学家 ($p=4$) 试图抓住他们右边的叉子(叉子 0)的情况。
我们还需要一些信号量来解决这个问题。假设我们有五个,每个叉子一个:sem_t forks[5]。
6.2 残缺的解决方案
我们尝试第一个解决方案。假设我们将每个信号量(在 forks 数组中)初始化为值 1。还假设每个哲学家都知道自己的数字 (p)。因此,我们可以编写 getforks() 和 putforks() 例程,代码如下所示。
| |
这个(残缺的)解决方案背后的直觉如下。为了获得叉子,我们只需抓住每个叉子上的“锁”:首先是左边的,然后是右边的。当我们吃完后,我们就释放它们。很简单,不是吗?不幸的是,在这种情况下,简单就意味着破碎。
如果每个哲学家碰巧在任何哲学家抓住右边的叉子之前抓住了他们左边的叉子,那么每个哲学家都会永远拿着一把叉子并等待另一把叉子。具体来说,哲学家0抓叉子0,哲学家1抓叉子1,哲学家2抓叉子2,哲学家3抓叉子3,哲学家4抓叉子4;所有的叉子都已获得,所有的哲学家都在等待另一位哲学家拥有的叉子。我们很快就会更详细地研究死锁;目前,可以肯定地说这不是一个有效的解决方案。
6.3 解决方案:打破依赖
要解决这个问题,最简单的方法就是改变至少一位哲学家获取分叉的方式;事实上,Dijkstra 本人就是这样解决这个问题的。具体来说,假设哲学家 4(编号最高者)以不同的顺序获取分叉。代码如下:
| |
由于最后一位哲学家会先抓右边,然后再抓左边,因此不会出现每位哲学家都抓到一个叉子,却只能等待另一个叉子的情况;等待的循环被打破了。
像这样的 “著名 “问题还有很多,比如抽烟者问题或睡觉的理发师问题。它们中的大多数只是思考并发问题的借口;其中有些问题的名字很吸引人。如果你有兴趣了解更多,或者只是想多练习并发思维,可以去查查这些问题。
7 如何实现信号量
最后,让我们使用低级同步原语、锁和条件变量来构建我们自己的信号量版本,称为Zemaphores。这个任务相当简单,代码如下所示。
| |
从代码中可以看出,我们只使用了一把锁和一个条件变量,再加上一个状态变量来跟踪信号量的值。
Zem_t结构体定义了一个信号量,其中包含了一个整数值value用于表示信号量的状态,一个条件变量cond用于线程间的同步通信,以及一个互斥锁lock用于保护共享数据。Zem_init函数用于初始化信号量,将初始值赋给value,并分别初始化条件变量和互斥锁。Zem_wait函数用于等待信号量,首先获取互斥锁,然后在一个循环中检查value是否小于等于 0,如果是则等待条件变量,直到被唤醒后再次检查。一旦value大于 0,就将其减一并释放互斥锁。Zem_post函数用于释放信号量,首先获取互斥锁,然后将value加一,以及唤醒等待在条件变量上的线程,最后释放互斥锁。
我们的 Zemaphore 和 Dijkstra 定义的纯信号量之间的一个细微差别是,我们不保持信号量的值(当为负时)反映等待线程的数量这一不变式;事实上,该值永远不会低于零。此行为更容易实现并且与当前的 Linux 实现相匹配。
TIP:小心泛化 因此,泛化的抽象技术在系统设计中非常有用,其中一个好的想法可以变得稍微更广泛,从而解决更大类别的问题。然而,泛化时要小心;正如Lampson警告我们的那样,“不要泛化;泛化通常是错误的”。
人们可以将信号量视为锁和条件变量的泛化;然而,是否需要这样的泛化?而且,考虑到在信号量之上实现条件变量的困难,也许这种泛化并不像您想象的那么普遍。
相关内容
 支付宝
支付宝 微信
微信